Формула Тейлора с остаточным членом в форме Лагранжа

1) Многочлен Тейлора.

Если f (x) дифференцируема в точке x ₀, то ее приращение в этой точке можно представить в виде:

f (x) - f (x ₀) = f ’(x ₀)(x – x ₀) + o (x – x ₀).

f (x) = 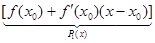+ o (x – x ₀).

P ₁(x) обладает следующими свойствами: P ₁(x ₀) = f (x ₀), P ’₁(x ₀) = f ’(x ₀). Рассмотрим теперь более общую задачу. Пусть f (x) n раз дифференцируема в точке x ₀, то есть имеет в точке n все производные до n -го порядка. Поставим задачу найти такой многочлен P_n (x) (степени £ n), что:

P_n (x ₀) = f (x ₀), P ’ _n (x ₀) = f ’(x ₀), P ’’ _n (x ₀) = f ’’(x ₀), …, P ⁽ⁿ⁾ _n (x ₀) = f ⁽ⁿ⁾(x ₀). (1)

Будем искать многочлен P_n (x) в виде:

P_n (x) = a ₀ + a ₁(x – x ₀) + a ₂(x – x ₀)² + a ₃(x – x ₀)³ + … + a_k (x – x ₀) ^k + … + a_n (x – x ₀) ⁿ. (2)

Покажем, что можно так выбрать коэффициенты a ₀, a ₁, …, a_n, что многочлен P_n (x) будет удовлетворять условию (1). Полагая в равенстве (2) x = x ₀ и учитывая первое из равенств (1), получим P_n (x ₀) = a ₀ = f ( x ₀). a ₀ = f (x ₀). Продифференцируем равенство (2).

P ’ _n (x) = a ₁ + 2 a ₂(x – x ₀) + 3 a ₃(x – x ₀)² + … + na _n(x – x ₀) ^{n -1}. (2’)

Положим в равенстве (2’) x = x ₀ и учтем второе условие из (1).

P ’ _n (x ₀) = a ₁ = f (x ₀).

a ₁ = .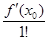

Продифференцируем равенство (2’):

P ’’ _n (x) = 2 a ₂ + 2×3 a ₃(x – x ₀) + … + n (n – 1) a _n(x – x ₀) ^{n -1}. (2’’)

Положим в полученном равенстве (2’’) x = x ₀ и учтем третье условие из (1).

P ’’ _n (x ₀) = 2 a ₂ = f ’’(x ₀).

a ₂ = .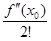

И так далее. После k –кратного дифференцирования равенства (2) получим:

P ^{( k )} _n (x) = k! a_k + 2 a_{k +1}(x – x ₀) + … + n (n - 1)…(n – k + 1)(x – x ₀) ^k. (2^{( k )})

Полагая здесь x = x ₀ и учитывая k +1–е условие из (1), получим:

P ^(k) _n (x ₀) = k! a_k = f ^(k)(x ₀).

a_k = 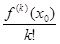(k = 0, 1, …, n), если принять обозначения f ⁽⁰⁾ = f, 0! = 1. Итак, мы нашли такие коэффициенты a_k, что многочлен

P_n (x) = f (x ₀) + 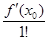(x – x ₀) + … + 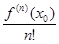(x – x ₀) ⁿ = 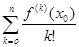(x – x ₀) ^k. (3)

удовлетворяет условиям (1). Многочлен (3) называется многочленом Тейлора для функции f (x).

Теорема 7.15. Пусть f (x) определена и n +1раз дифференцируема в окрестности точки x ₀. Пусть x – любое значение аргумента из этой окрестности, не равное x ₀, p – любое вещественное число. Тогда $ точка x Î (x ₀, x):

R_{n +1}(x) = f (x) – P_n (x) = 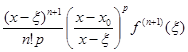. (7)