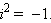Базис любого конечномерного подпространства 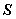 в унитарном или евклидовом пространстве
в унитарном или евклидовом пространстве 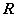 является невырожденным рядом векторов и потому согласно теореме 2 предыдущего параграфа может быть проортогонализирован и пронормирован. Таким образом, в любом конечномерном подпространстве
является невырожденным рядом векторов и потому согласно теореме 2 предыдущего параграфа может быть проортогонализирован и пронормирован. Таким образом, в любом конечномерном подпространстве 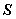 (и, в частности, во всем пространстве
(и, в частности, во всем пространстве 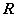 , если оно конечномерно) существует ортонормированный базис.
, если оно конечномерно) существует ортонормированный базис.
Пусть 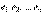 – ортонормированный базис пространства
– ортонормированный базис пространства 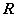 . Обозначим через
. Обозначим через 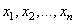 координаты произвольного вектора
координаты произвольного вектора 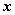 в этом базисе:
в этом базисе:
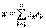 Умножая обе части этого равенства справа на
Умножая обе части этого равенства справа на 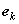 и учитывая ортонормированность базиса, легко найдем:
и учитывая ортонормированность базиса, легко найдем:
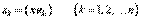 ,
,
т. е. в ортонормированном базисе координата вектора равна скалярному произведению его на соответствующий базисный орт
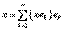 . (41)
. (41)
Пусть 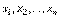 и
и 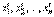 суть соответственно координаты одного и того же вектора
суть соответственно координаты одного и того же вектора 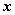 в двух различных ортонормированных базисах
в двух различных ортонормированных базисах 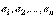 и
и 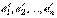 унитарного пространства
унитарного пространства 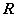 . Формулы преобразования координат имеют вид
. Формулы преобразования координат имеют вид
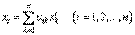 . (42)
. (42)
При этом коэффициенты 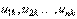 , образующие
, образующие 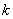 -й столбец матрицы
-й столбец матрицы 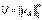 , являются, как нетрудно видеть, координатами вектора
, являются, как нетрудно видеть, координатами вектора 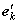 в базисе
в базисе 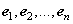 . Поэтому, записывая в координатах [см. (10)] условия ортонормированности базиса
. Поэтому, записывая в координатах [см. (10)] условия ортонормированности базиса 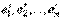 , получим соотношения
, получим соотношения
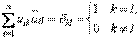 (43)
(43)
Преобразование (42), у которого коэффициенты удовлетворяют условию (43), называется унитарным, а соответствующая матрица 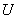 – унитарной матрицей. Таким образом, в
– унитарной матрицей. Таким образом, в 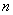 -мерном унитарном пространстве переход от одного ортонормированного базиса к другому ортонормированному осуществляется при помощи унитарного преобразования координат.
-мерном унитарном пространстве переход от одного ортонормированного базиса к другому ортонормированному осуществляется при помощи унитарного преобразования координат.
Пусть дано 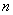 -мерное евклидово пространство
-мерное евклидово пространство 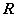 . Переход от одного ортонормированного базиса в
. Переход от одного ортонормированного базиса в 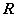 к другому осуществляется при помощи преобразования координат
к другому осуществляется при помощи преобразования координат
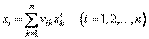 , (44)
, (44)
коэффициенты которого связаны между собой соотношениями
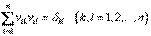 . (45)
. (45)
Такое преобразование координат называется ортогональным, а соответствующая матрица 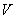 – ортогональной матрицей.
– ортогональной матрицей.
Отметим интересную матричную запись процесса ортогонализации. Пусть 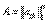 – произвольная неособенная матрица
– произвольная неособенная матрица 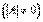 с комплексными элементами. Рассмотрим унитарное пространство
с комплексными элементами. Рассмотрим унитарное пространство 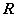 с ортонормированным базисом
с ортонормированным базисом 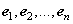 и определим линейно независимые векторы
и определим линейно независимые векторы 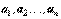 равенством
равенством
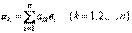 .
.
Подвергнем векторы 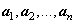 процессу ортогонализации. Полученный ортонормированный базис в
процессу ортогонализации. Полученный ортонормированный базис в 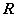 обозначим через
обозначим через 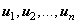 . Пусть при этом
. Пусть при этом
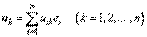 Тогда
Тогда 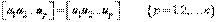 ,т. е.
,т. е. 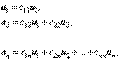
где 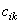
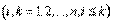 – некоторые комплексные числа. Полагая
– некоторые комплексные числа. Полагая 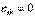 при
при 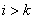
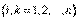 , будем иметь
, будем иметь
 . Переходя здесь к координатам и вводя верхнюю треугольную матрицу
. Переходя здесь к координатам и вводя верхнюю треугольную матрицу 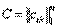 и унитарную матрицу
и унитарную матрицу 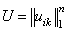 , получим:
, получим:
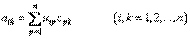 ,или
,или 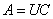 . (*)
. (*)
Согласно этой формуле произвольная неособенная матрица 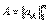 представима в виде произведения унитарной матрицы
представима в виде произведения унитарной матрицы 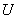 на верхнюю треугольную
на верхнюю треугольную 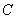 .
.
Так как процесс ортогонализации однозначно определяет векторы 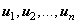 с точностью до скалярных множителей
с точностью до скалярных множителей 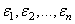
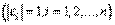 , то в формуле множители
, то в формуле множители 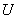 и
и 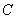 определяются однозначно с точностью до диагонального множителя
определяются однозначно с точностью до диагонального множителя 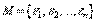 :
:
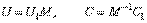 . В этом можно убедиться и непосредственно.
. В этом можно убедиться и непосредственно.
Замечание 1. Если 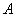 – вещественная матрица, то в формуле (*) множители
– вещественная матрица, то в формуле (*) множители 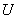 и
и 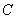 можно выбрать вещественными. В этом случае
можно выбрать вещественными. В этом случае 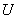 – ортогональная матрица.
– ортогональная матрица.
Замечание 2. Формула (*) сохраняет свою силу и для особенной матрицы 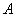
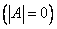 . В этом можно убедиться, полагая
. В этом можно убедиться, полагая 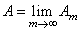 , где
, где 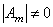
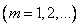 .
.
Тогда 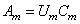
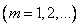 . Выделяя из последовательности
. Выделяя из последовательности 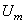 сходящуюся подпоследовательность
сходящуюся подпоследовательность 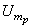
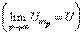 и переходя к пределу, из равенства
и переходя к пределу, из равенства 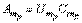 при
при 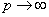 , получим искомое разложение
, получим искомое разложение 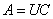 . Однако в случае
. Однако в случае 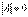 множители U и C уже не определяются однозначно с точностью до диагонального множителя
множители U и C уже не определяются однозначно с точностью до диагонального множителя 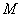 .
.
Замечание 3. Вместо (*) можно получить формулу
A=DW, (**)
Где D – нижняя треугольная, a W – унитарная матрица. Действительно, применяя установленную ранее формулу (*) к транспонированной матрице A’
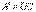 и полагая
и полагая 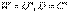 , получим (**).
, получим (**).
Квадратичной формой 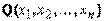 от n неизвестных
от n неизвестных 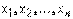 называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Обозначая коэффициент при
называется сумма, каждое слагаемое которой является или квадратом одного из этих неизвестных, или произведением двух разных неизвестных. Обозначая коэффициент при 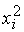 через
через 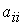 , а при произведении
, а при произведении 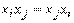
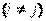 – через
– через 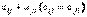 , квадратичную форму Q можно представить в виде
, квадратичную форму Q можно представить в виде
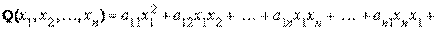
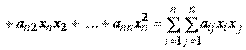 .
.
Симметричная матрица 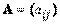 называется матрицей квадратичной формы Q.
называется матрицей квадратичной формы Q.
Пример. Написать матрицу квадратичной формы
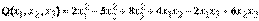 .
.
Здесь 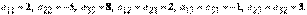
Следовательно,
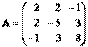
В векторно-матричной форме квадратичная форма имеет вид
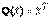 A
A 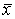 , где
, где 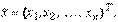 Если в квадратичной форме
Если в квадратичной форме 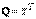 А
А 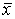 неизвестные подвергнуть линейному преобразованию
неизвестные подвергнуть линейному преобразованию 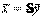 , где
, где 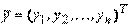 ,
,
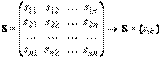
получится квадратичная форма 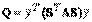 с матрицей
с матрицей 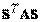 . Матрица S называется матрицей линейного преобразования неизвестных. Если S – невырожденная матрица, то линейное преобразование неизвестных также называется невырожденным.
. Матрица S называется матрицей линейного преобразования неизвестных. Если S – невырожденная матрица, то линейное преобразование неизвестных также называется невырожденным.
Рангом квадратичной формы 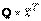 А
А 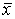 называется ранг матрицы А. Ранг квадратичной формы не изменяется при невырожденных преобразованиях неизвестных.
называется ранг матрицы А. Ранг квадратичной формы не изменяется при невырожденных преобразованиях неизвестных.
Для каждой квадратичной формы 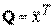 А
А 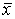 можно подобрать такое линейное преобразование неизвестных
можно подобрать такое линейное преобразование неизвестных 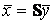 с ортогональной матрицей S (квадратная матрица S называется ортогональной,если
с ортогональной матрицей S (квадратная матрица S называется ортогональной,если 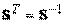 ), что матрица квадратичной формы
), что матрица квадратичной формы 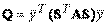 будет диагональной, т. е. квадратичная форма приводится к сумме квадратов
будет диагональной, т. е. квадратичная форма приводится к сумме квадратов
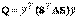
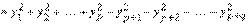 . (8.1)
. (8.1)
Закон инерции квадратичных форм. Приводя квадратичную форму к сумме квадратов разными способами, мы будем получать в формуле (8.1) разные коэффициенты. Однако существует следующее важное обстоятельство (закон инерции квадратичных форм): если квадратичная форма приводится к сумме квадратов в двух разных базисах, то число членов с положительными коэффициентами, так же как и число членов с отрицательными коэффициентами, в обоих случаях одно и то же. Легко увидеть, что сумма 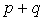 равна рангу
равна рангу 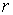 квадратичной формы
квадратичной формы 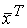 А
А 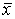 . Разность
. Разность 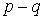 называется сигнатурой квадратичной формы
называется сигнатурой квадратичной формы 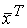 А
А 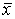 .
.
Квадратичная форма 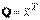 А
А 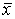 называется:
называется:
1) положительно(отрицательно)-определенной, если для любого ненулевого 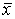 выполняется неравенство
выполняется неравенство 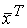 А
А 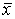 > 0 (
> 0 (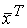 А
А 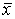 < 0);
< 0);
2 знакопеременной, если существуют такие 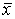 и
и 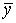 , что
, что 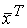 А
А 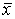 > 0
> 0 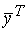 А
А 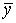 <0;
<0;
3) положительно(отрицательно)-полуопределенной, или квазизнакоопределенной, если для всех 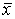
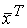 А
А 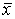 ³ 0 (
³ 0 (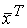 А
А 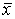 £ 0), но имеется отличный от нуля вектор
£ 0), но имеется отличный от нуля вектор 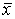 , для которого
, для которого 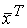 А
А 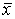 = 0.
= 0.
Ясно, что положительно-определенная квадратичная форма приводится к сумме квадратов с положительными коэффициентами, а положительно-полуопределенная форма – с неотрицательными коэффициентами. Важным условием положительной определенности квадратичной формы является следующий критерий (критерий Сильвестра).
Для того чтобы квадратичная форма 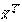 А
А 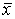 была положительно-определенной, необходимо и достаточно, чтобы были положительны все главные, или угловые, миноры
была положительно-определенной, необходимо и достаточно, чтобы были положительны все главные, или угловые, миноры

матрицы 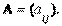 Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма
Теперь нетрудно найти и условия отрицательной определенности квадратичной формы. Для того чтобы квадратичная форма 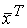 А
А 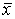 была отрицательно-определенной необходимо и достаточно, чтобы все главные миноры нечетного порядка были отрицательны, а все главные миноры четного порядка – положительны.
была отрицательно-определенной необходимо и достаточно, чтобы все главные миноры нечетного порядка были отрицательны, а все главные миноры четного порядка – положительны.
Теорема 8.1. Квадратичная форма 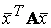 положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны).
положительно (отрицательно) определена тогда и только тогда, когда все собственные значения матрицы А положительны (отрицательны). 
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a=c; b=d
2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число a+c+i(b+d)
3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac-bd+i(ad+bc)
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
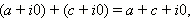 |
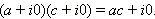 |
Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается 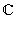 . Мы установили, что
. Мы установили, что 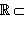
 , а именно
, а именно 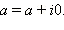
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i 3 = 3 i. Чисто мнимое число i 1 = 1 i = i обладает удивительным свойством:
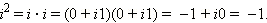 |
Таким образом,
|
С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства 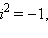 то и перемножать эти числа можно как многочлены. В самом деле,
то и перемножать эти числа можно как многочлены. В самом деле,
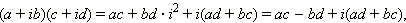 |
то есть как раз получается нужная формула.
Модулем комплексного числа называется длина вектора, соответствующего этому числу:
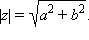
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором
 величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
Если число z = a + bi, то число 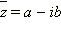 называется комплексно сопряжённым с числом z.
называется комплексно сопряжённым с числом z.
Комплексно сопряжённое число обозначается 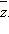 Для этого числа справедливы соотношения:
Для этого числа справедливы соотношения:
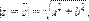 |
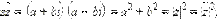 |
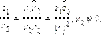 |
Заметим, что последнее соотношение сводит операцию деления комплексных чисел к умножению 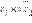 и последующему делению на действительное число
и последующему делению на действительное число 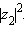
 2015-04-20
2015-04-20 781
781