Свойства базиса, естественный базис, координаты вектора в заданном базисе

Итак установлено, что в пространстве Rⁿ существует система из n линейно независимых векторов, а любые n +1 вектора линейно зависимы.

Число n — размерность пространства Rⁿ.

Определение. Любая упорядоченная линейно независимая система n векторов 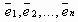пространства арифметических векторов Rⁿ называется базисом в Rⁿ.

Нетрудно показать, что любой вектор 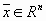единственным образом выражается через векторы базиса: 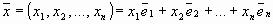. (На лекции единственность доказана).

Числа 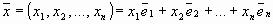называют координатами вектора 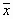в базисе .

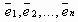Линейно независимая система векторов

образует базис в Rⁿ, который называют естественным базисом в Rⁿ.