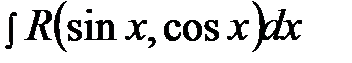 ,
,
когда в числителе и знаменателе могут присутствовать целые степени 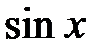 и
и 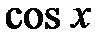 .
.
1) Универсальным методом сведения такого типа интегралов к интегралам от рациональных дробей являются так называемая универсальная тригонометрическая подстановка 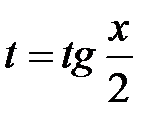 . При этом
. При этом 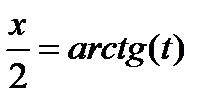 ,
, 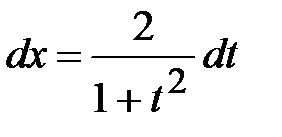
Выразим 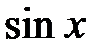 и
и 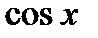 через t
через t
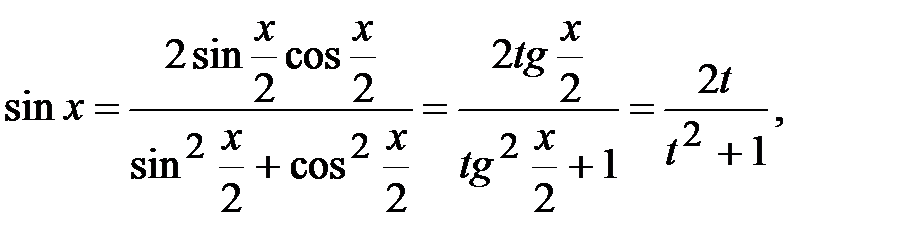

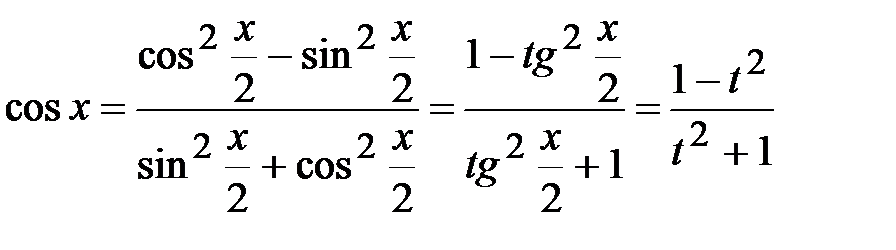 .
.
В результате исходный интеграл примет вид:
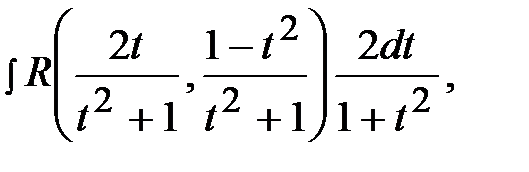
то есть получили интеграл от рациональной дроби относительно переменной t.
Универсальная подстановка работает всегда. Она, как правило, приводит к громоздким вычислениям, поэтому на практике стараются по возможности использовать более простые приемы.
2) Самая простая ситуация – интегралы вида:
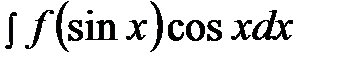 и
и 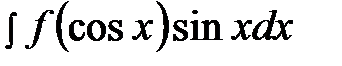
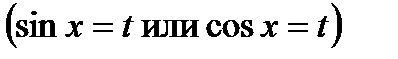
Интегралы вида:
3) 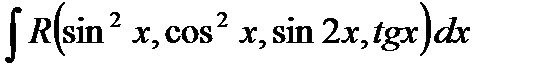
Такие интегралы рационализируются подстановкой 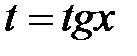 .
.
При этом 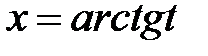 ,
, 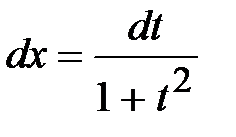 ,
,
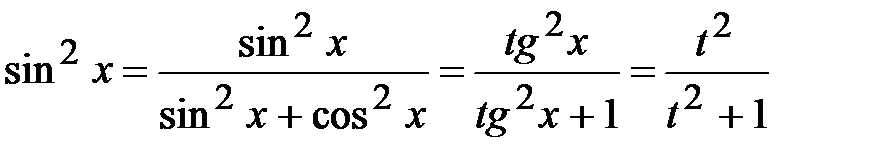 ,
,
 ,
,
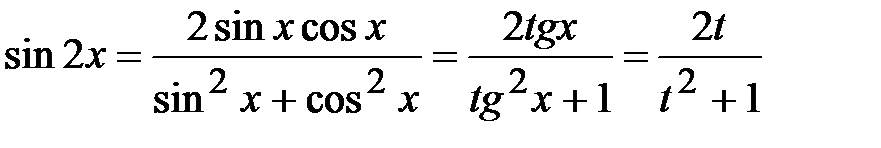 .
.
В результате получим интеграл от рациональной дроби относительно t:
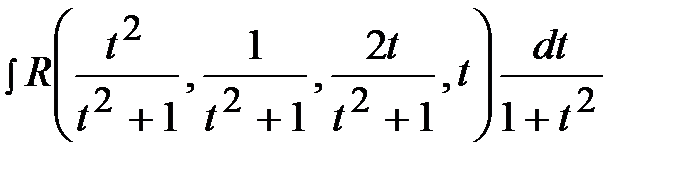 .
.
4) Интегралы вида 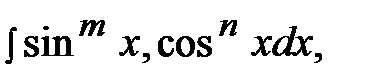 где n и m – целые
где n и m – целые
Такие интегралы находятся по-разному в зависимости от четности n и m или (и) их знаков. Возможны три случая:
а) Хотя бы одно из чисел m и n – нечетное.
Пусть, например, 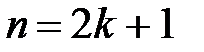 . Тогда
. Тогда
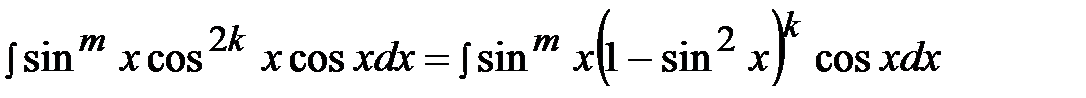
Получили интеграл вида 2), который рационализируется подстановкой 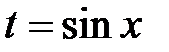 . В результате получим интеграл
. В результате получим интеграл 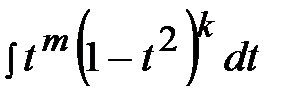 ,
,
который сводится к табличным.
б) m и n – оба четные и неотрицательные. В этом случае используются формулы понижения степени:
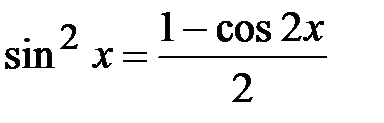 ,
, 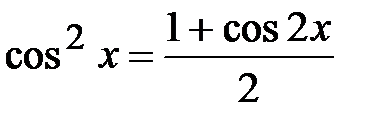 ,
, 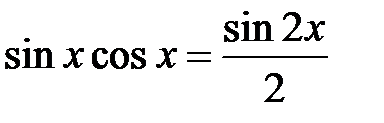 .
.
Пусть 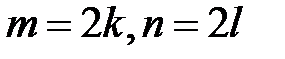 . Тогда
. Тогда
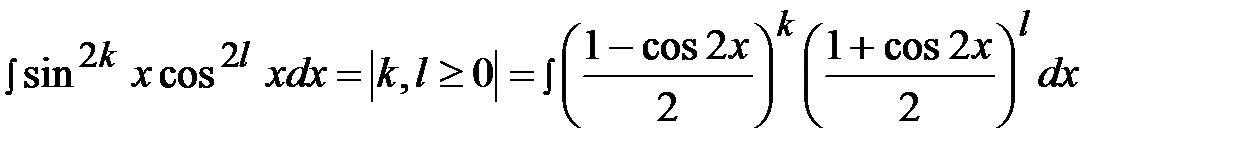
В подынтегральном выражении будут присутствовать слагаемые с четными и нечетными степенями 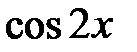 .
.
Слагаемые с нечетными степенями интегрируются как в пункте а), а к слагаемым с четными степенями снова применим формулы понижения степени.
в) m и n – оба четные и среди них есть отрицательное. В этом случае используется подстановка 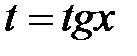 , поскольку это есть частный случай пункта 3).
, поскольку это есть частный случай пункта 3).
В интегралах от произведений 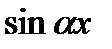 и
и 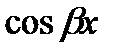 используются школьные формулы преобразования произведения в сумму функций.
используются школьные формулы преобразования произведения в сумму функций.
Пример 34. 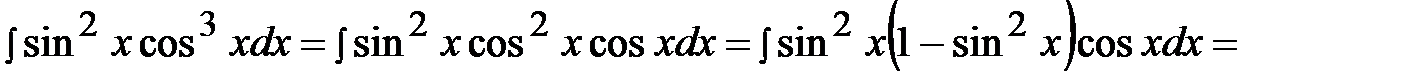
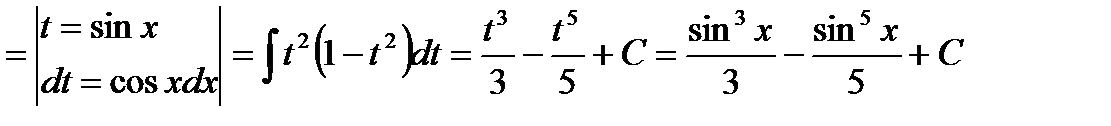 .
.
Пример 35. 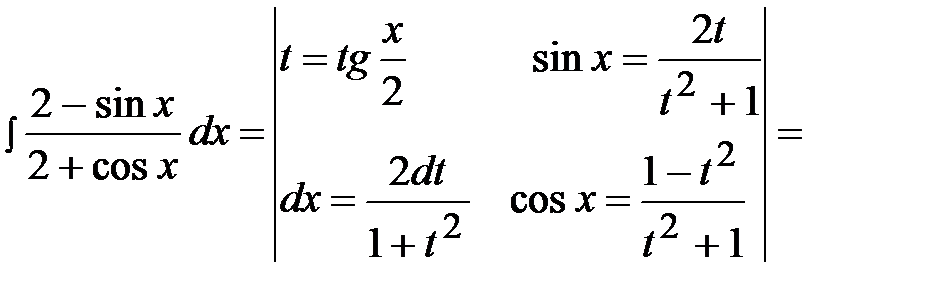
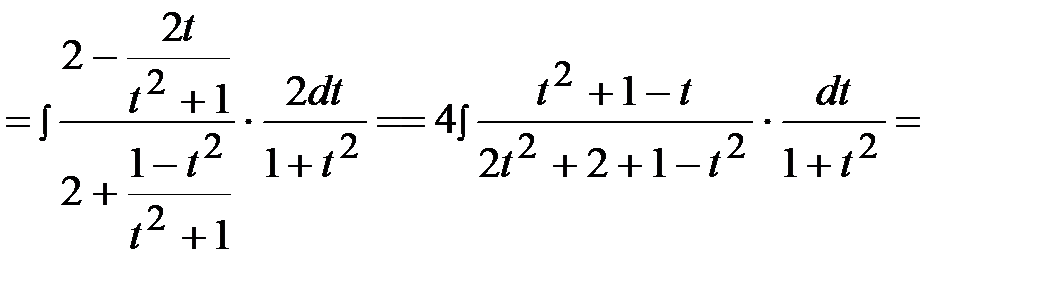
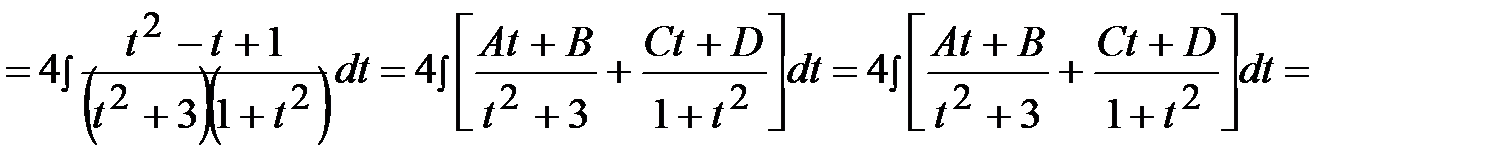 .
.
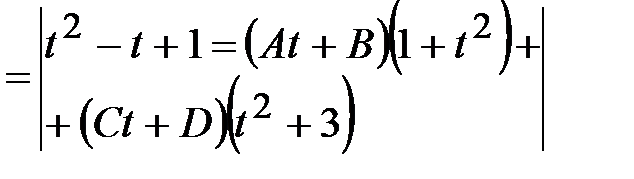
приравниваем коэффициенты при одинаковых степенях:
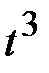 :
: 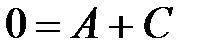
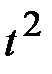 :
: 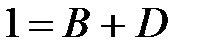
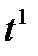 :
: 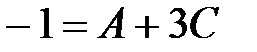
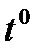 :
: 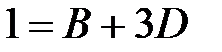
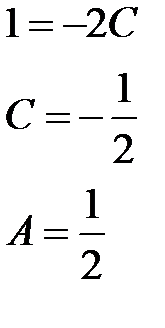
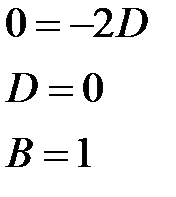
Тогда получим:
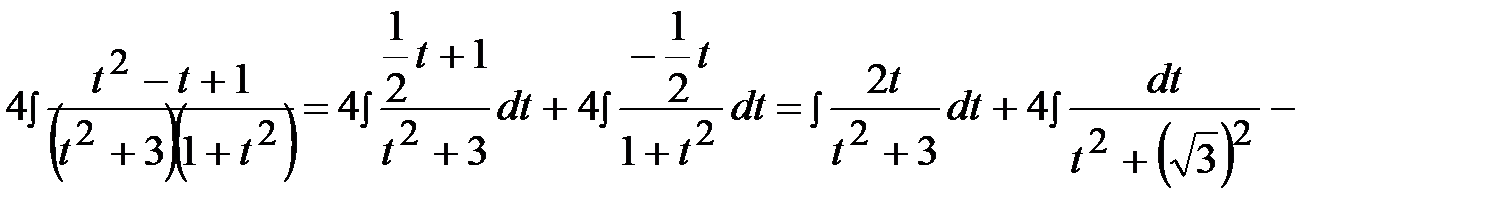
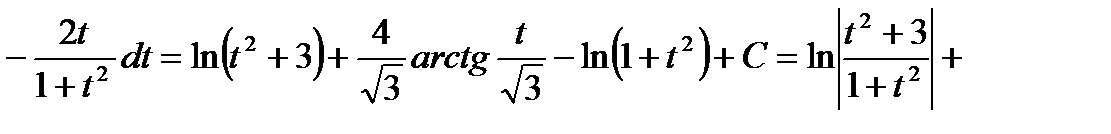
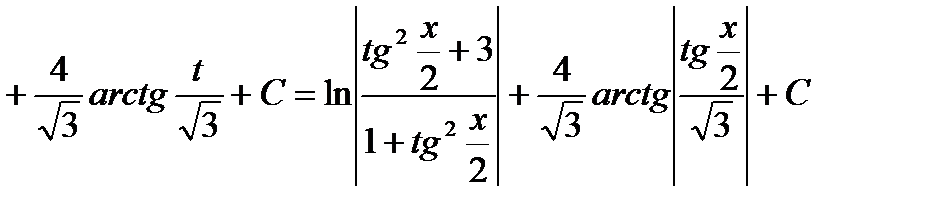 .
.
Пример 36.
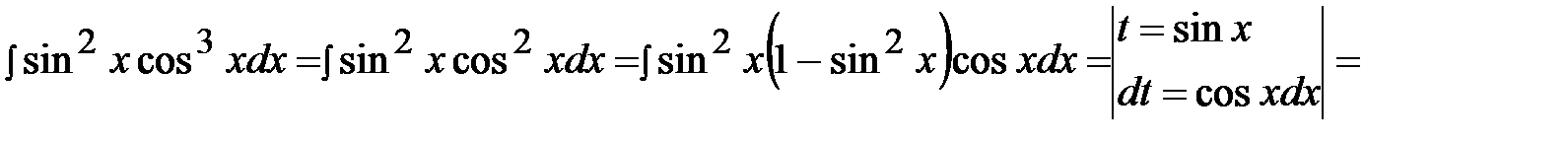
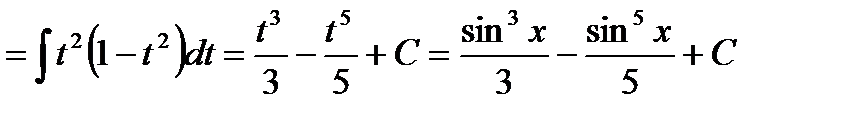 .
.
Пример 37.
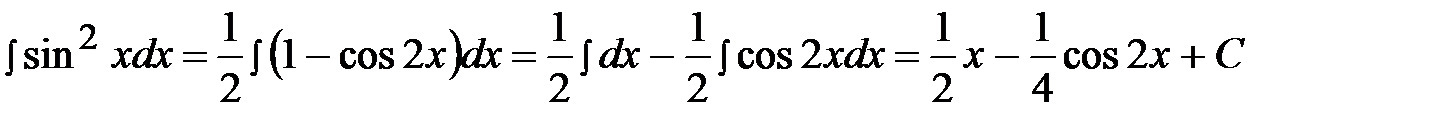 .
.
Пример 38.
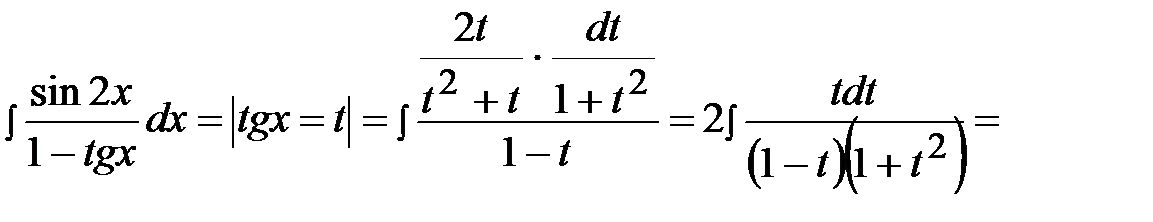
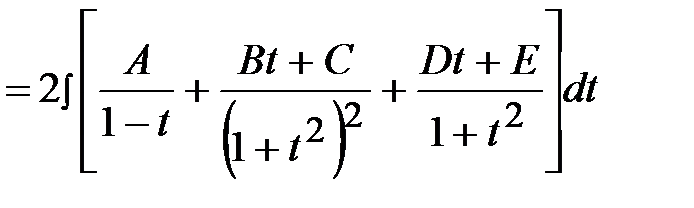 .
.
Рекомендуется самостоятельно дорешать пример.
Пример 39.
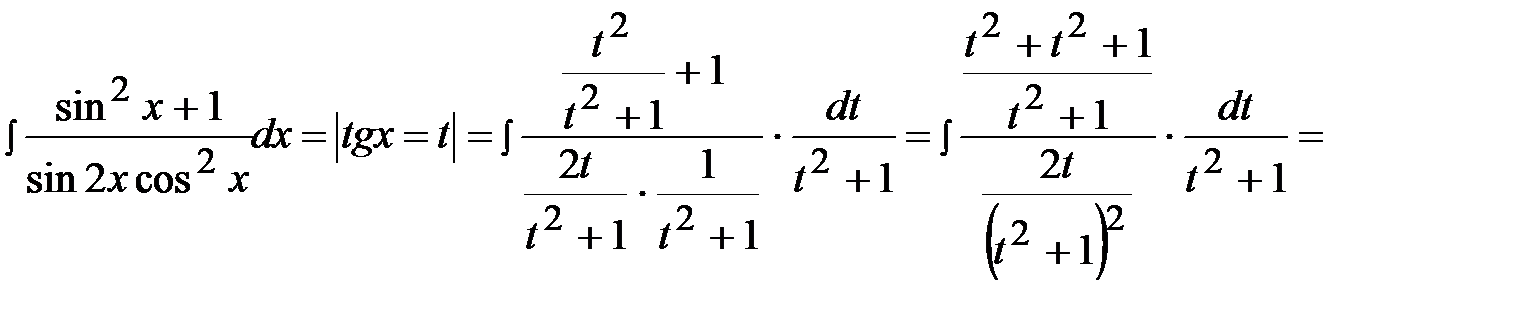
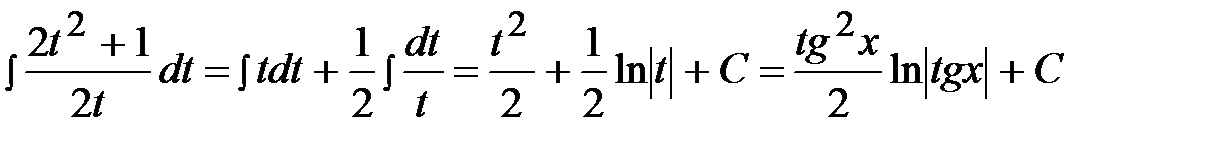 .
.
Вопросы для самопроверки
1. Какая подстановка называется универсальной тригонометрической и почему?
2. Какие тригонометрические формулы используются при интегрировании выражений, содержащих произведение неотрицательных четных степеней 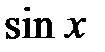 и
и 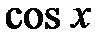 ?
?
3. Как находятся интегралы в случае, когда в произведении 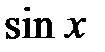 на
на 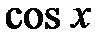 присутствует нечетная степень?
присутствует нечетная степень?
4. На каких формулах основано вычисление интегралов от функций 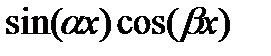 ,
, 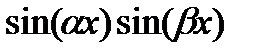 ,
, 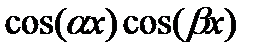 ?
?
5. В каких случаях используется подстановка 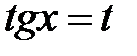 ?
?
6.2 Примеры для самостоятельного решения
1. 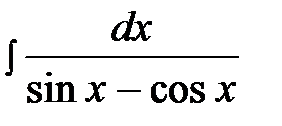 2.
2. 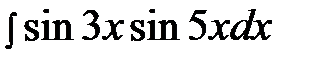
3. 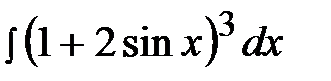 4.
4. 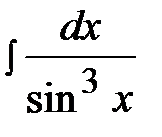
Варианты индивидуальных заданий
Пример 1.
1.1. 
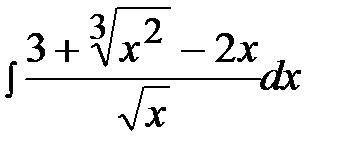 1.16.
1.16. 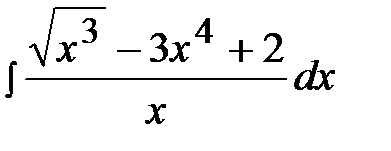
1.2. 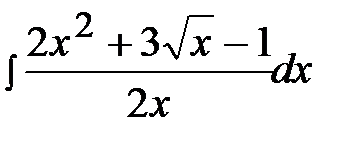 1.17.
1.17. 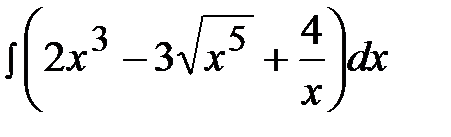
1.3. 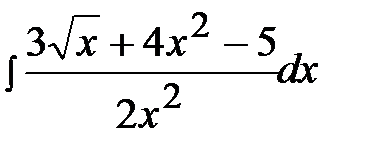 1.18.
1.18. 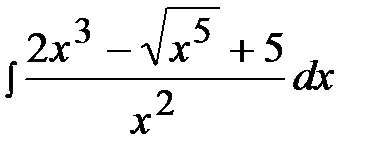
1.4. 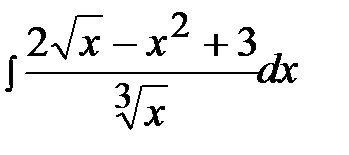 1.19.
1.19. 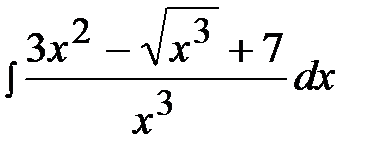
1.5. 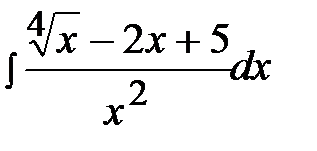 1.20.
1.20. 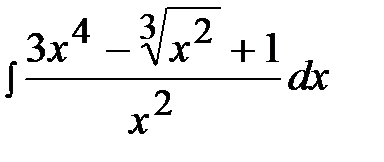
1.6. 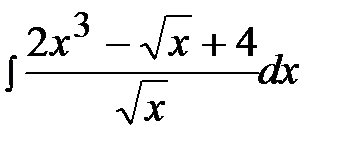 1.21.
1.21. 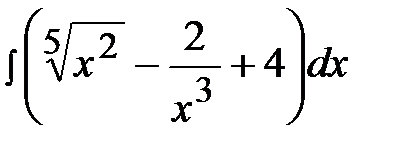
1.7. 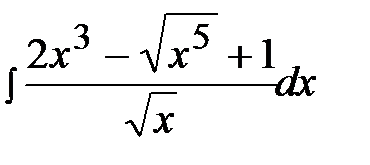 1.22.
1.22. 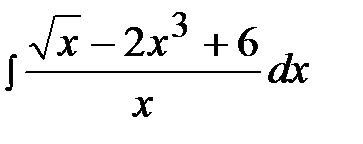
1.8. 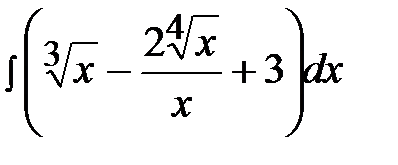 1.23.
1.23. 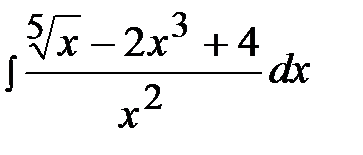
1.9. 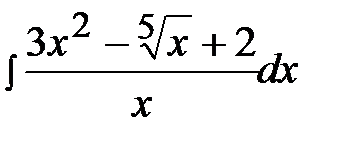 1.24.
1.24. 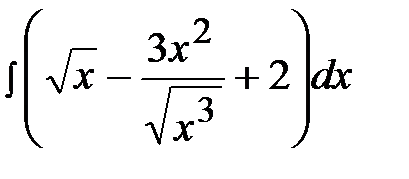
1.10. 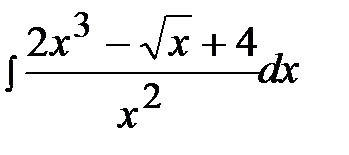 1.25.
1.25. 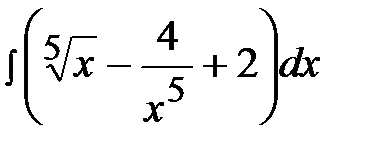
1.11. 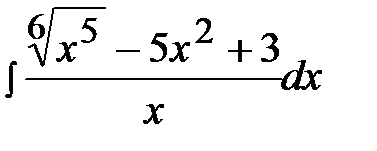 1.26.
1.26. 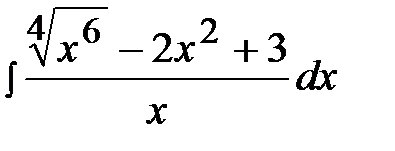
1.12. 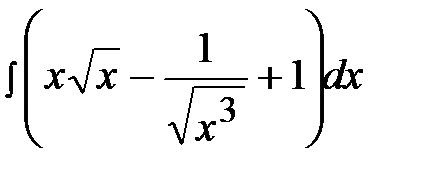 1.27.
1.27. 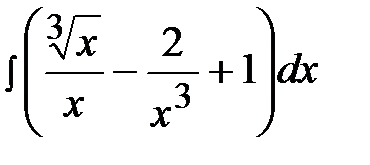
1.13. 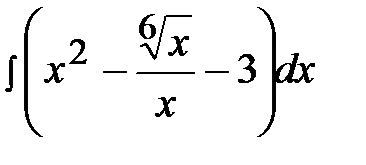 1.28.
1.28. 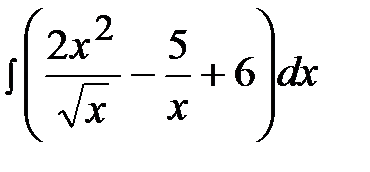
1.14. 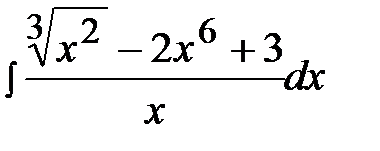 1.29.
1.29. 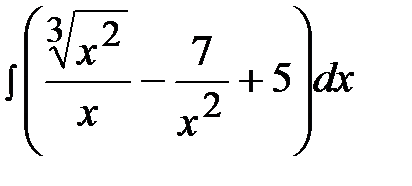
1.15. 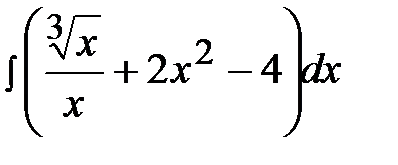 1.30.
1.30. 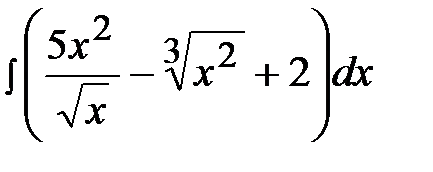
Пример 2.
2.1. 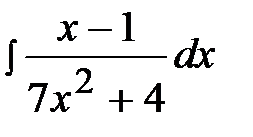 2.16.
2.16. 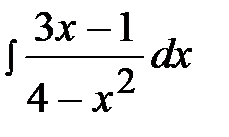
2.2. 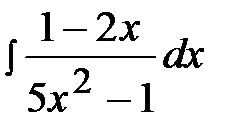 2.17.
2.17. 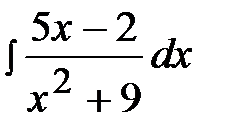
2.3. 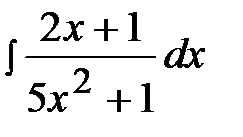 2.18.
2.18. 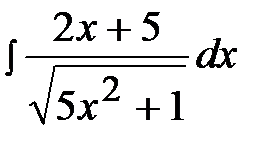
2.4. 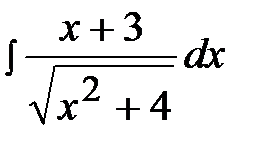 2.19.
2.19. 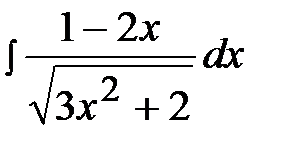
2.5. 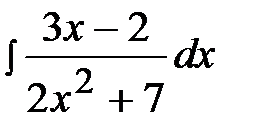 2.20.
2.20. 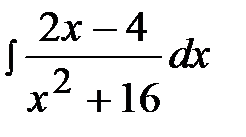
2.6. 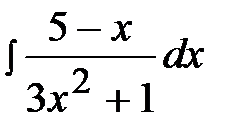 2.21.
2.21. 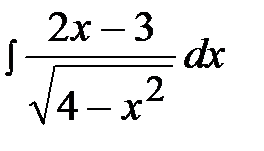
2.7. 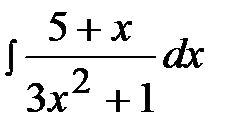 2.22.
2.22. 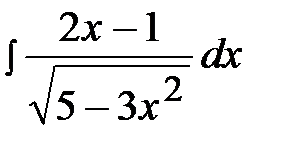
2.8. 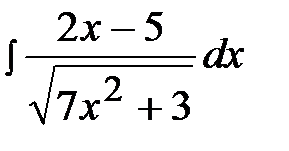 2.23.
2.23. 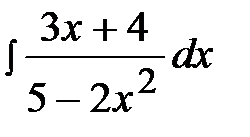
2.9. 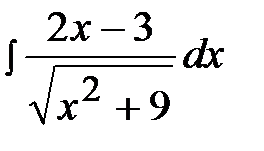 2.24.
2.24. 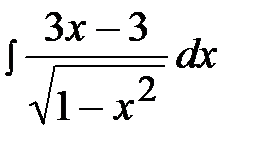
2.10. 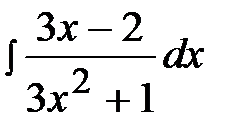 2.25.
2.25. 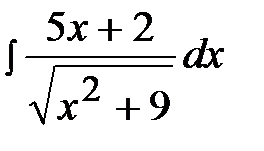
2.11. 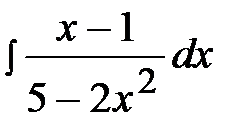 2.26.
2.26. 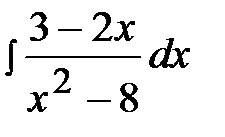
2.12. 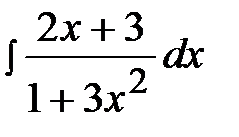 2.27.
2.27. 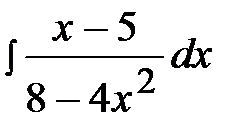
2.13. 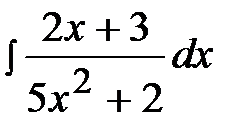 2.28.
2.28. 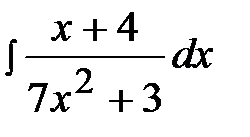
2.14. 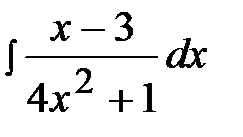 2.29.
2.29. 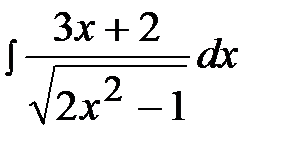
2.15. 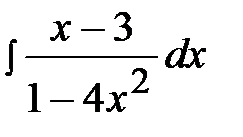 2.30.
2.30. 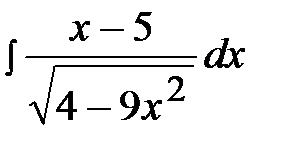
Пример 3.
3.1. 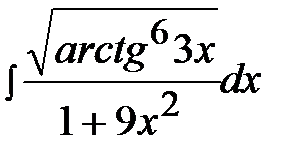 3.16.
3.16. 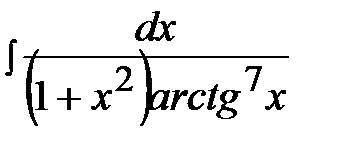
3.2. 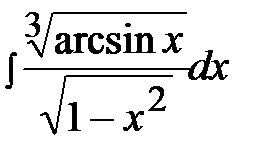 3.17.
3.17. 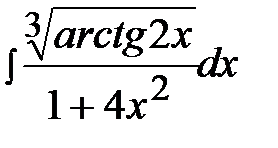
3.3. 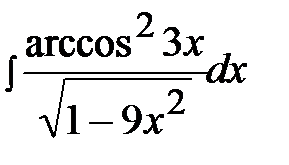 3.18.
3.18. 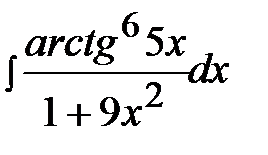
3.4. 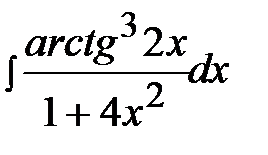 3.19.
3.19. 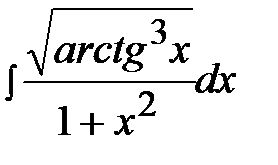
3.5 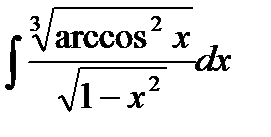 3.20.
3.20. 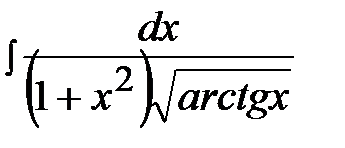
3.6. 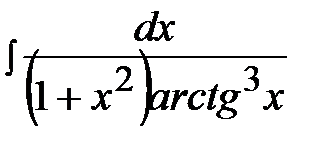 3.21.
3.21. 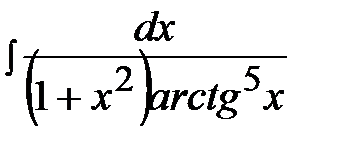
3.7. 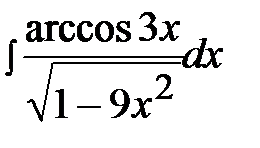 3.22.
3.22. 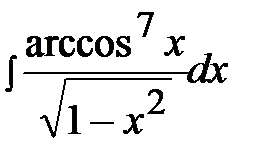
3.8. 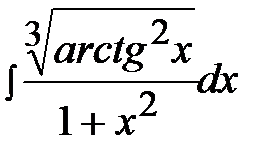 3.23.
3.23. 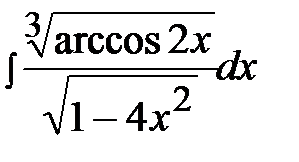
3.9. 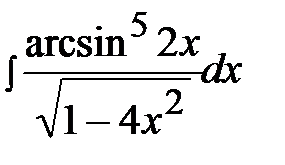 3.24.
3.24. 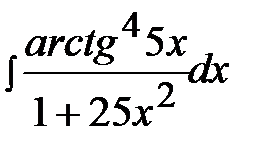
3.10. 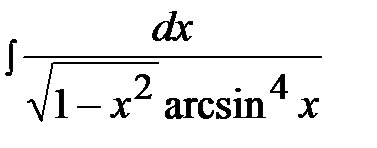 3.25.
3.25. 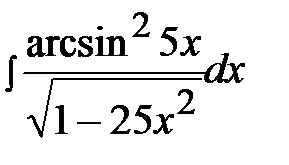
3.11. 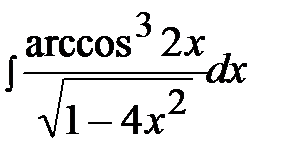 3.26.
3.26. 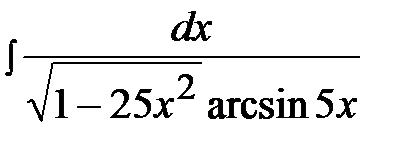
3.12. 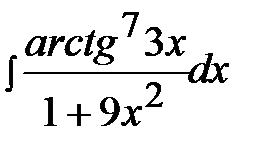 3.27.
3.27. 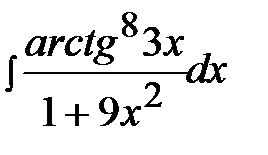
3.13. 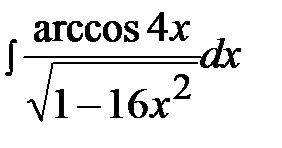 3.28.
3.28. 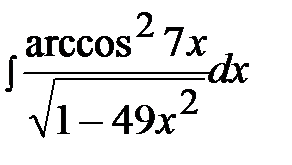
3.14. 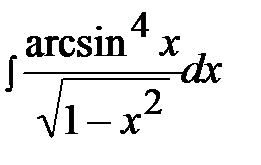 3.29
3.29 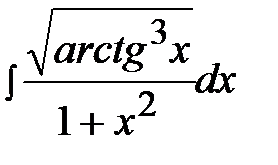
3.15. 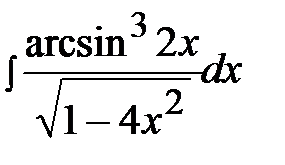 3.30.
3.30. 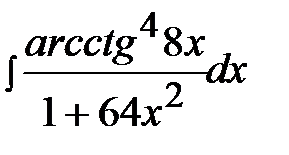
Пример 4.
4.1. 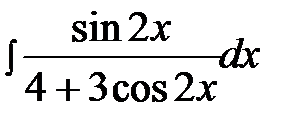 4.16.
4.16. 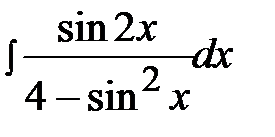
4.2. 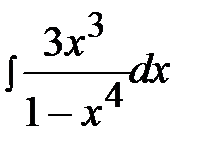 4.17.
4.17. 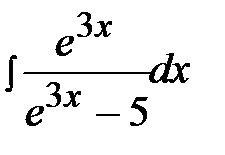
4.3. 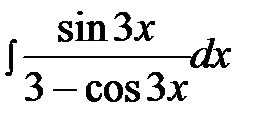 4.18.
4.18. 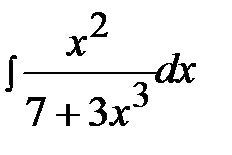
4.4. 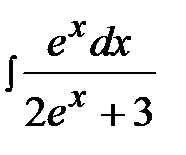 4.19.
4.19. 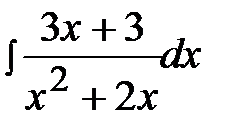
4.5. 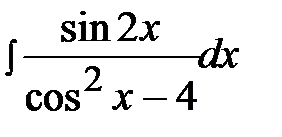 4.20
4.20 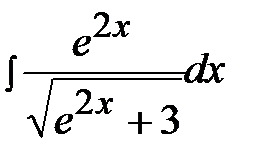
4.6. 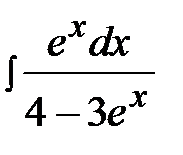 4.21.
4.21. 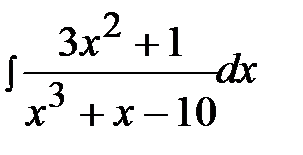
4.7. 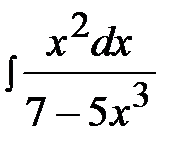 4.22.
4.22. 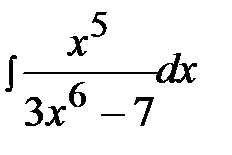
4.8. 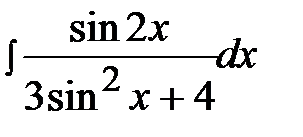 4.23.
4.23. 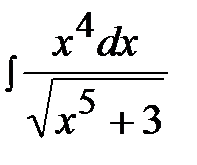
4.9. 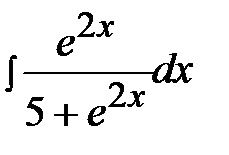 4.24.
4.24. 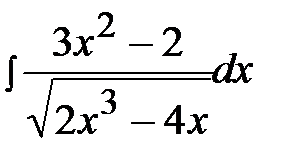
4.10. 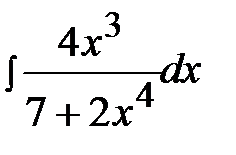 4.25.
4.25. 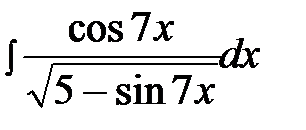
4.11. 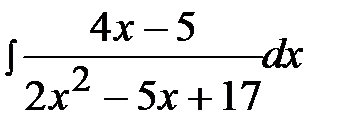 4.26.
4.26. 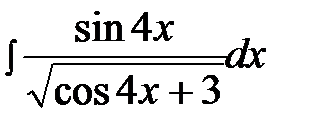
4.12. 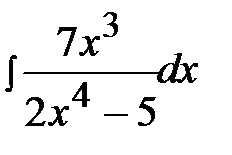 4.27.
4.27. 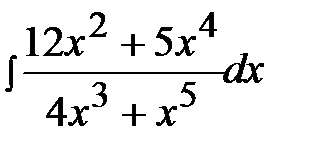
4.13. 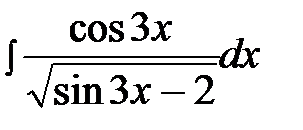 4.28.
4.28. 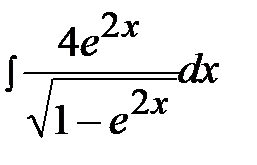
4.14. 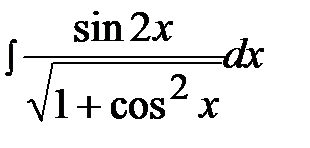 4.29.
4.29. 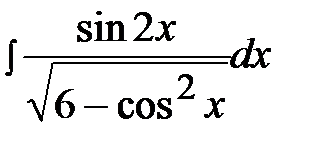
4.15. 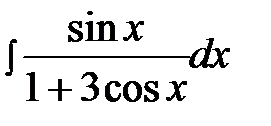 4.30.
4.30. 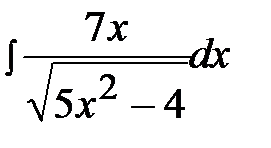
Пример 5.
5.1. 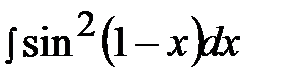 5.16.
5.16. 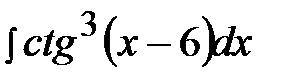
5.2. 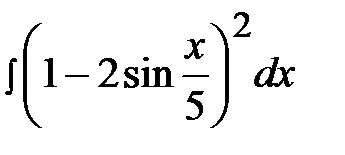 5.17.
5.17. 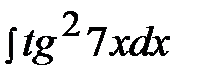
5.3. 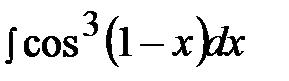 5.18.
5.18. 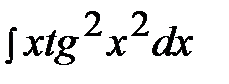
5.4. 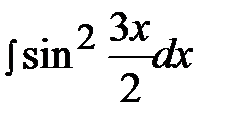 5.19.
5.19. 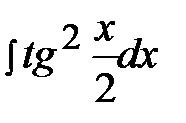
5.5. 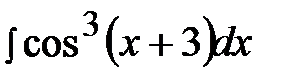 5.20.
5.20. 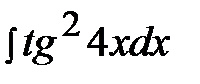
5.6. 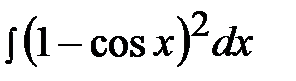 5.21.
5.21. 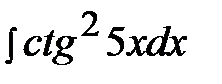
5.7. 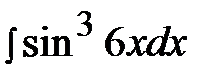 5.22.
5.22. 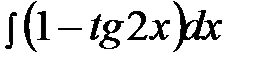
5.8. 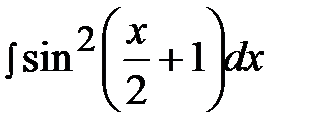 5.23.
5.23. 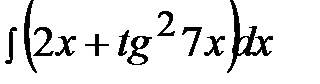
5.9. 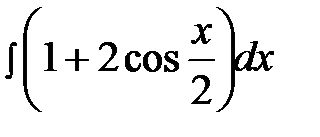 5.24.
5.24. 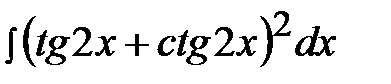
5.10. 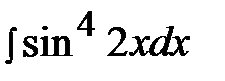 5.25.
5.25. 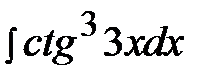
5.11. 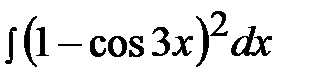 5.26.
5.26. 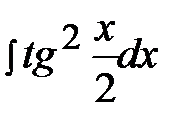
5.12. 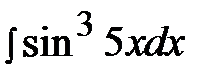 5.27.
5.27. 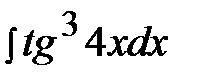
5.13. 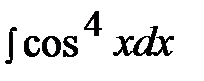 5.28.
5.28. 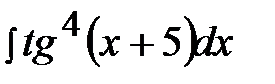
5.14. 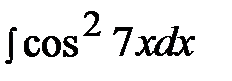 5.29.
5.29. 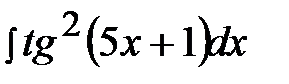
5.15. 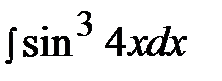 5.30.
5.30. 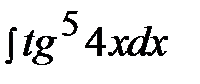
Пример 6.
6.1. 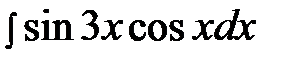 6.16.
6.16. 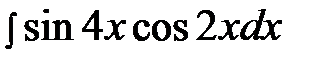
6.2. 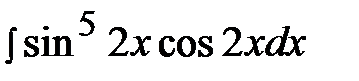 6.17.
6.17. 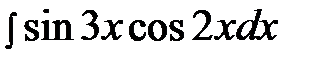
6.3. 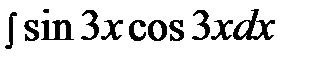 6.18.
6.18. 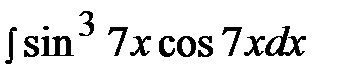
6.4. 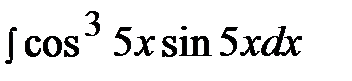 6.19.
6.19. 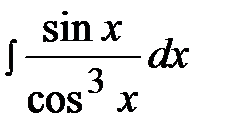
6.5. 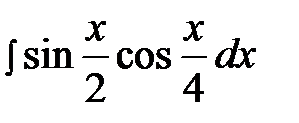 6.20.
6.20. 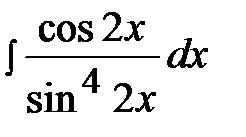
6.6. 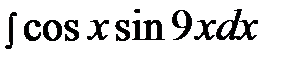 6.21.
6.21. 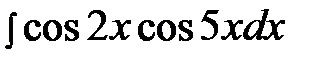
6.7. 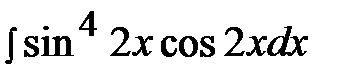 6.22.
6.22. 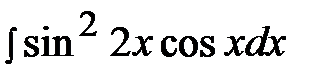
6.8. 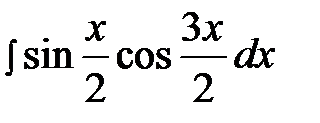 6.23.
6.23. 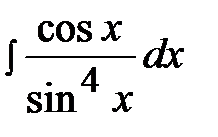
6.9. 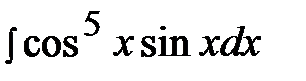 6.24.
6.24. 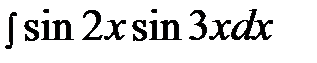
6.10. 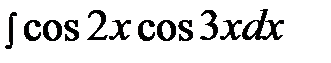 6.25.
6.25. 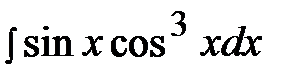
6.11. 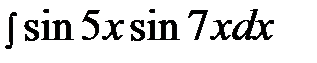 6.26.
6.26. 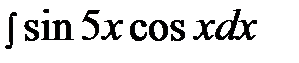
6.12. 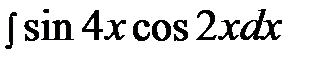 6.27.
6.27. 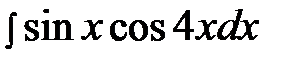
6.13. 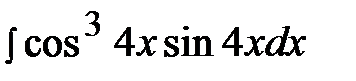 6.28.
6.28. 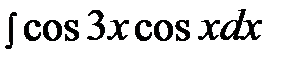
6.14. 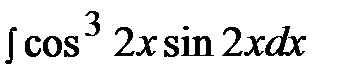 6.29.
6.29. 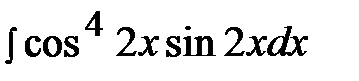
6.15. 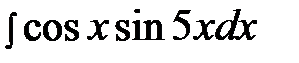 6.30.
6.30. 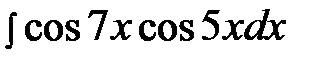
Примеры 7.
7.1. 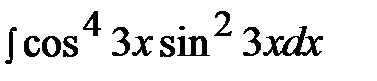 7.16.
7.16. 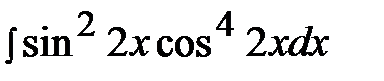
7.2. 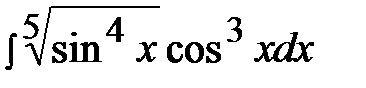 7.17.
7.17. 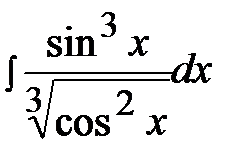
7.3. 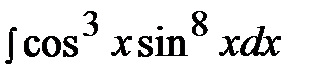 7.18.
7.18. 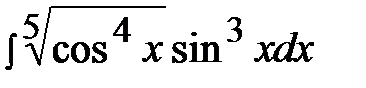
7.4. 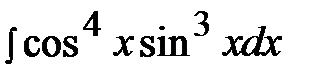 7.19.
7.19. 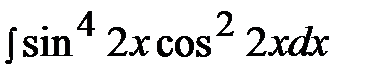
7.5. 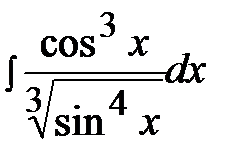 7.20.
7.20. 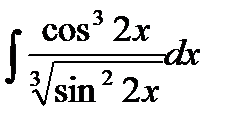
7.6. 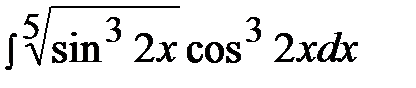 7.21.
7.21. 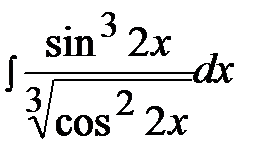
7.7. 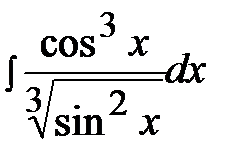 7.22.
7.22. 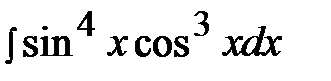
7.8. 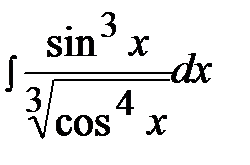 7.23.
7.23. 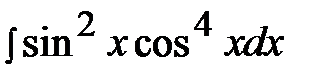
7.9. 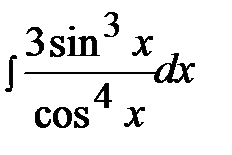 7.24.
7.24. 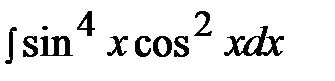
7.10. 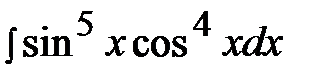 7.25.
7.25. 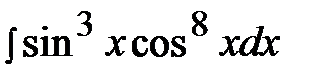
7.11. 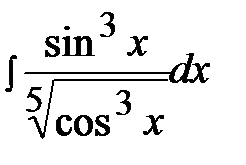 7.26.
7.26. 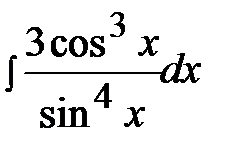
7.12. 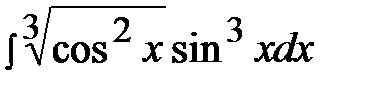 7.27.
7.27. 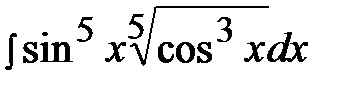
7.13. 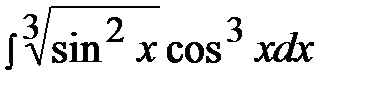 7.28.
7.28. 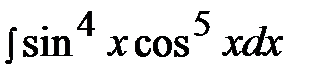
7.14. 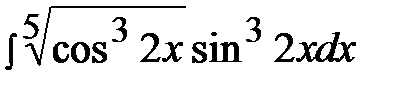 7.29.
7.29. 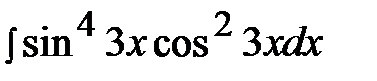
7.15. 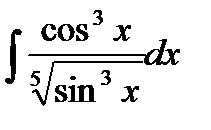 7.30.
7.30. 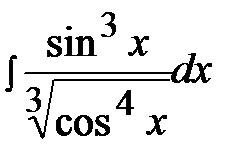
Пример 8.
8.1. 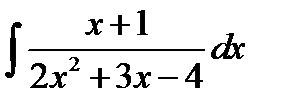 8.16.
8.16. 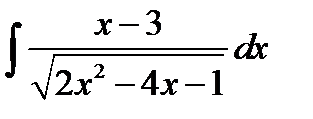
8.2. 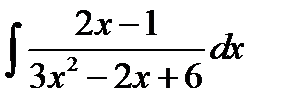 8.17.
8.17. 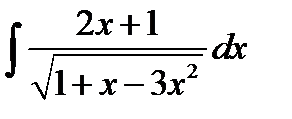
8.3. 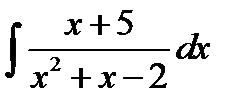 8.18.
8.18. 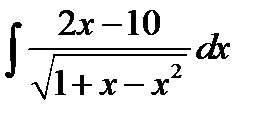
8.4. 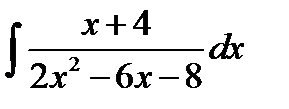 8.19.
8.19. 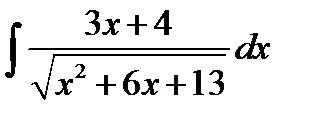
8.5. 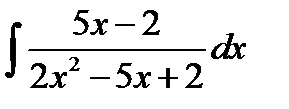 8.20.
8.20. 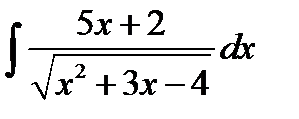
8.6. 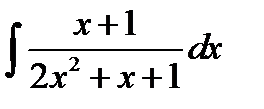 8.21.
8.21. 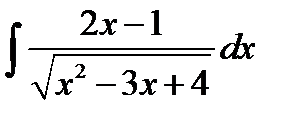
8.7. 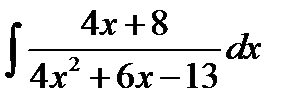 8.22.
8.22. 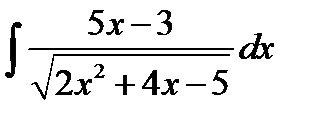
8.8. 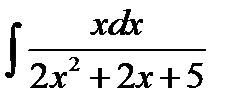 8.23.
8.23. 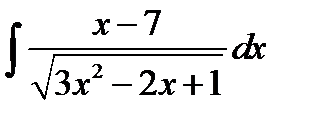
8.9. 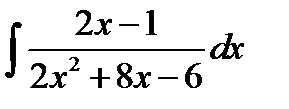 8.24.
8.24. 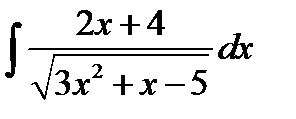
8.10. 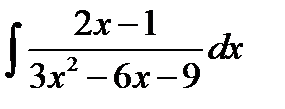 8.25.
8.25. 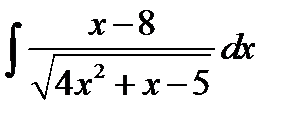
8.11. 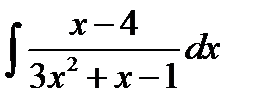 8.26.
8.26. 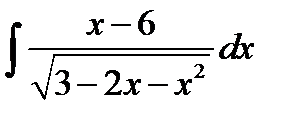
8.12. 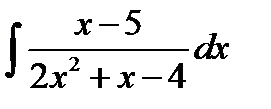 8.27.
8.27. 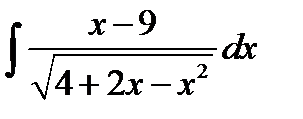
8.13. 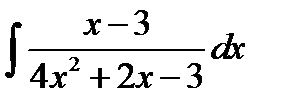 8.28.
8.28. 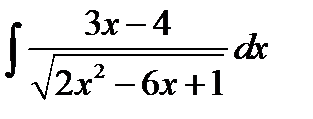
8.14. 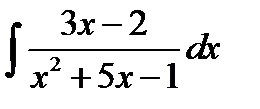 8.29.
8.29. 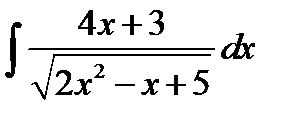
8.15. 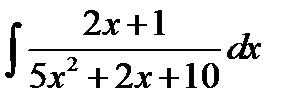 8.30.
8.30. 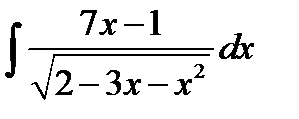
Пример 9.
9.1. 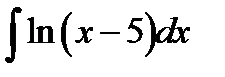 9.16.
9.16. 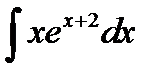
9.2. 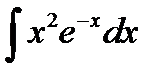 9.17.
9.17. 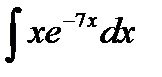
9.3. 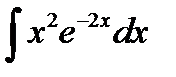 9.18.
9.18. 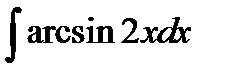
9.4. 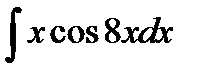 9.19.
9.19. 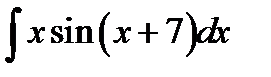
9.5. 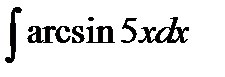 9.20.
9.20. 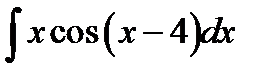
9.6. 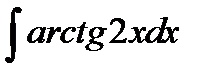 9.21.
9.21. 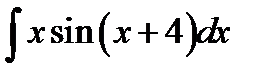
9.7. 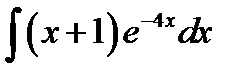 9.22.
9.22. 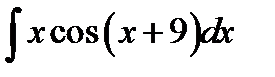
9.8. 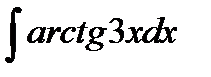 9.23.
9.23. 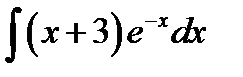
9.9. 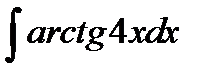 9.24.
9.24. 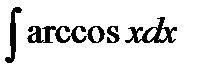
9.10. 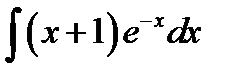 9.25.
9.25. 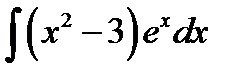
9.11. 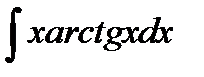 9.26.
9.26. 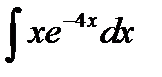
9.12. 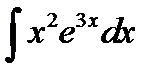 9.27.
9.27. 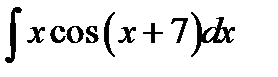
9.13. 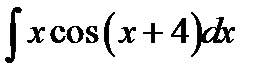 9.28.
9.28. 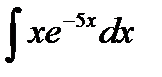
9.14. 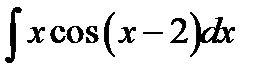 9.29.
9.29. 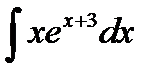
9.15. 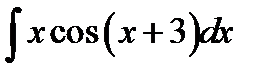 9.30.
9.30. 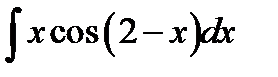
Пример10.
10.1. 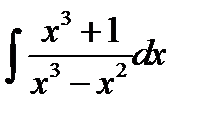 10.16.
10.16. 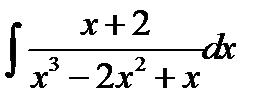
10.2. 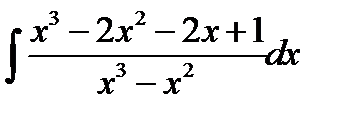 10.17.
10.17. 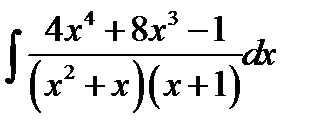
10.3. 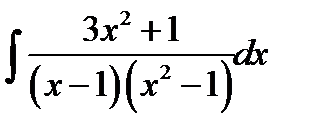 10.18.
10.18. 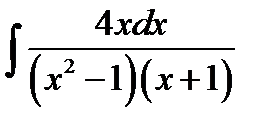
10.4. 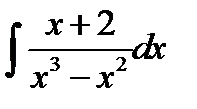 10.19.
10.19. 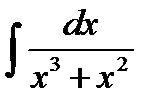
10.5. 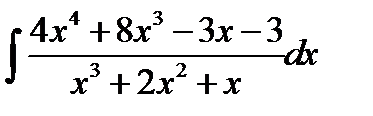 10.20.
10.20. 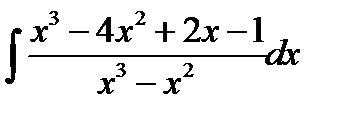
10.6. 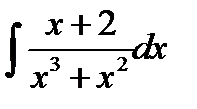 10.21.
10.21. 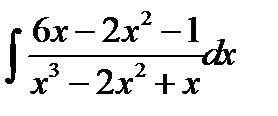
10.7. 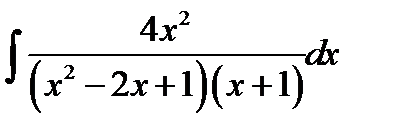 10.22.
10.22. 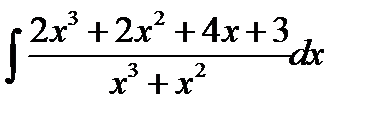
10.8. 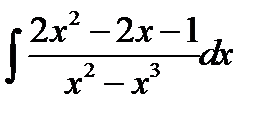 10.23.
10.23. 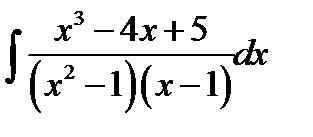
10.9. 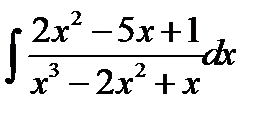 10.24.
10.24. 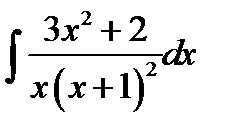
10.10. 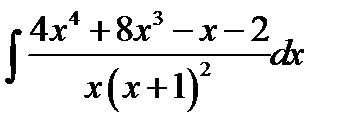 10.25.
10.25. 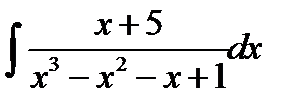
10.11. 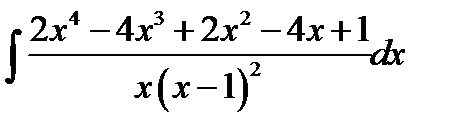 10.26.
10.26. 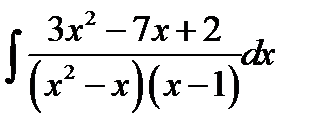
10.12. 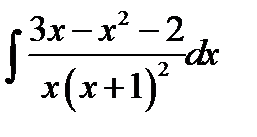 10.27.
10.27. 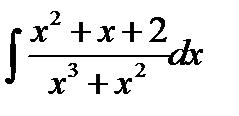
10.13. 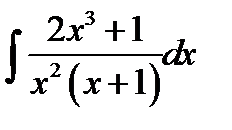 10.28.
10.28. 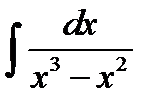
10.14. 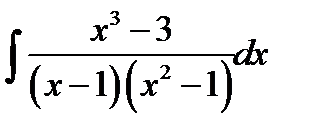 10.29.
10.29. 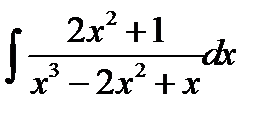
10.15. 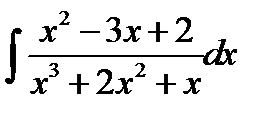 10.30.
10.30. 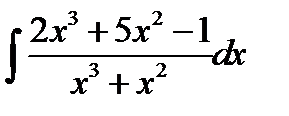
Пример 11.
11.1. 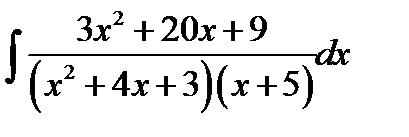 11.16.
11.16. 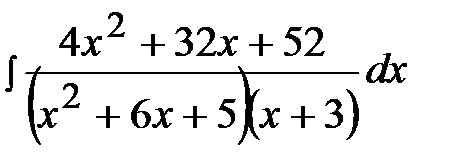
11.2. 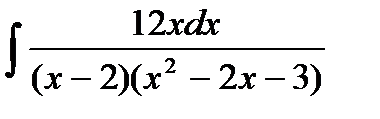 11.17.
11.17. 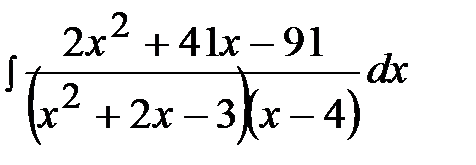
11.3. 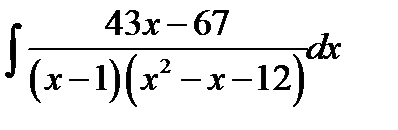 11.18.
11.18. 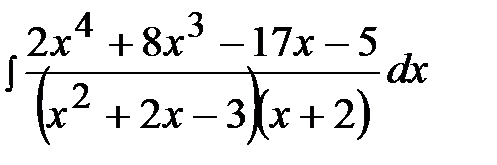
11.4. 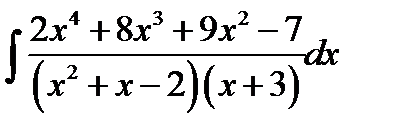 11.19.
11.19. 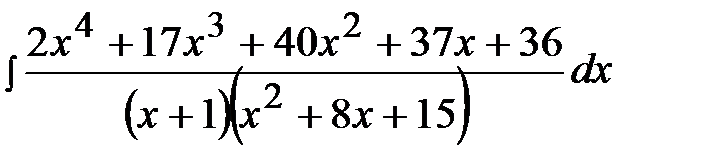
11.5. 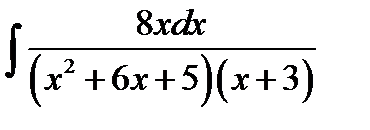 11.20.
11.20. 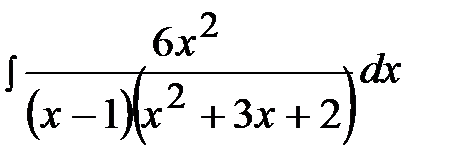
11.6. 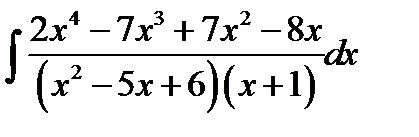 11.21.
11.21. 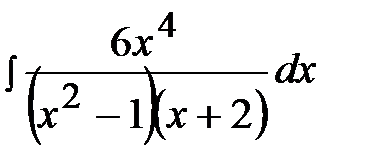
11.7. 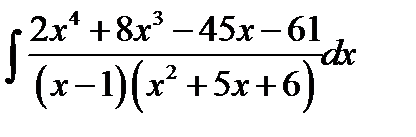 11.22.
11.22. 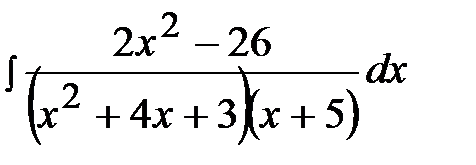
11.8. 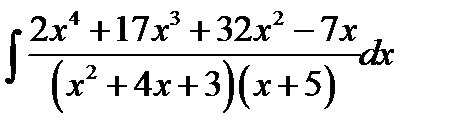 11.23.
11.23. 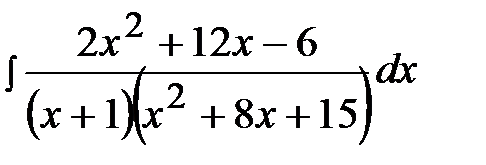
11.9 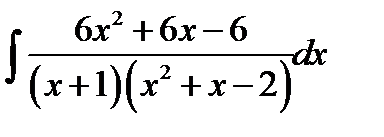 11.24.
11.24. 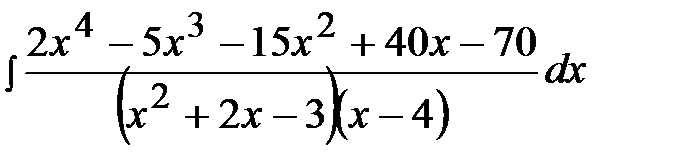
11.10. 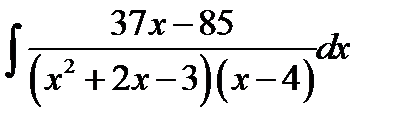 11.25.
11.25. 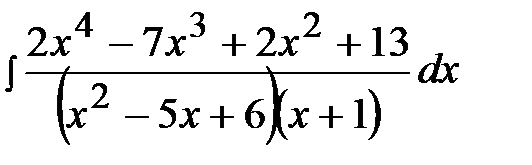
11.11. 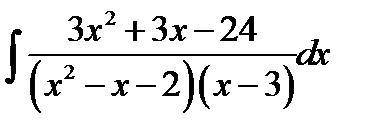 11.26.
11.26. 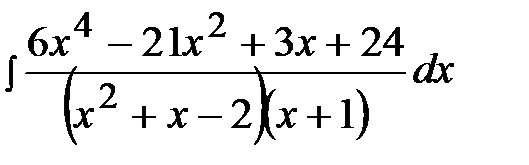
11.12. 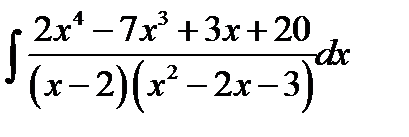 11.27.
11.27. 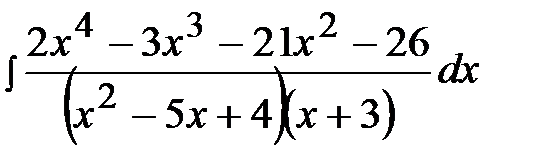
11.13. 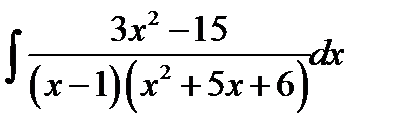 11.28.
11.28. 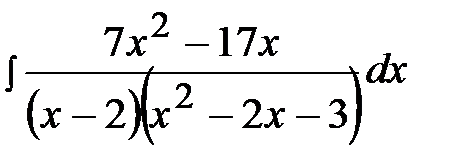
11.14. 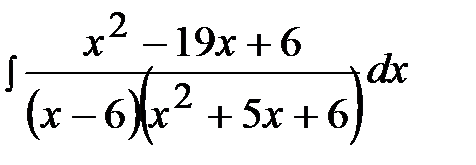 11.29.
11.29. 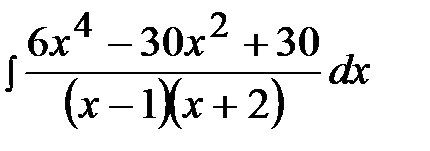
11.15. 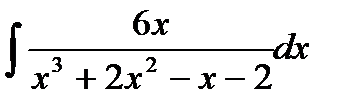 11.30.
11.30. 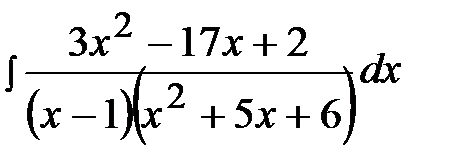
Пример 12.
12.1. 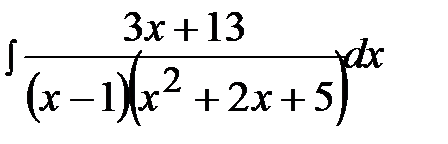 12.16.
12.16. 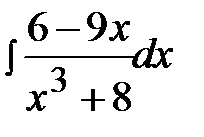
12.2. 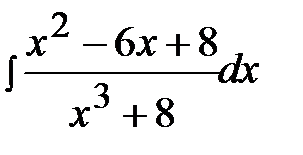 12.17.
12.17. 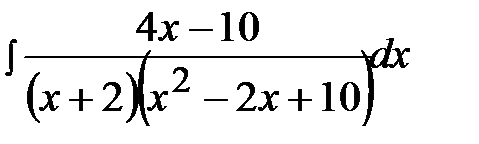
12.3. 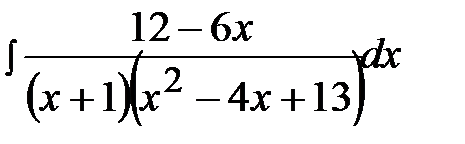 12.18.
12.18. 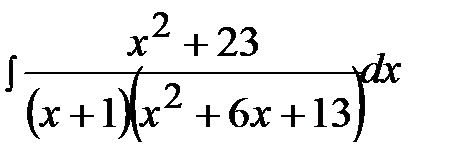
12.4. 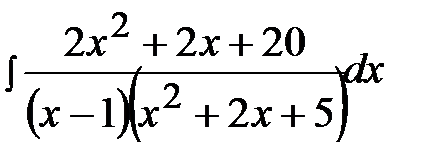 12.19.
12.19. 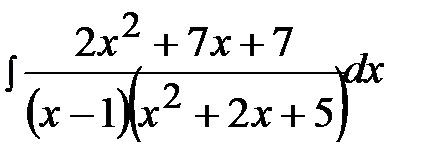
12.5. 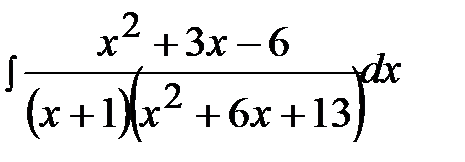 12.20.
12.20. 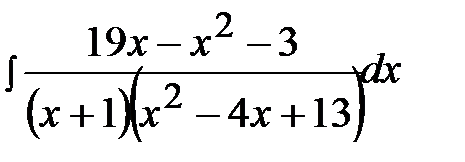
12.6. 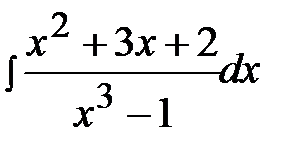 12.21.
12.21. 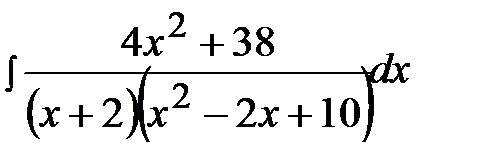
12.7. 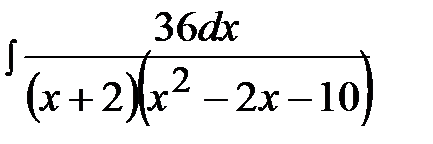 12.22.
12.22. 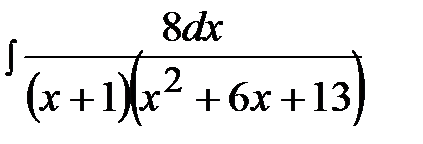
12.8. 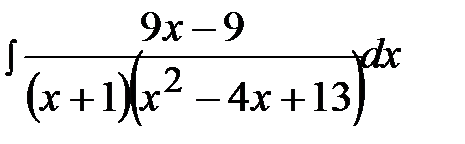 12.23.
12.23. 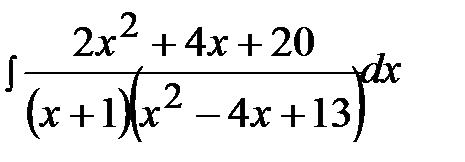
12.9. 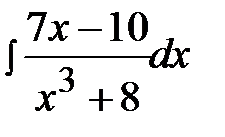 12.24.
12.24. 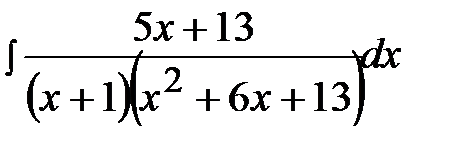
12.10. 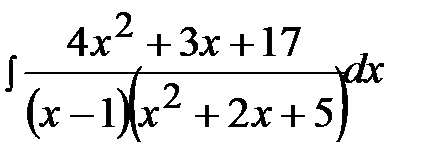 12.25
12.25 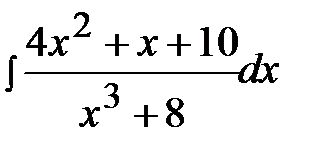
12.11. 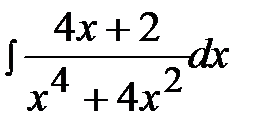 12.26
12.26 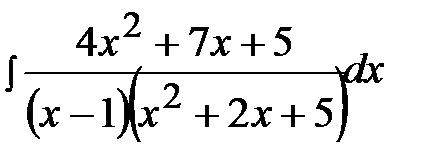
12.12. 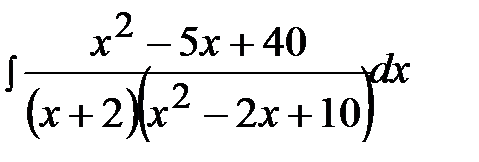 12.27
12.27 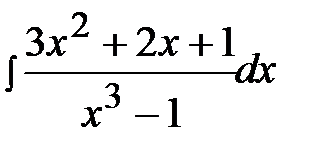
12.13. 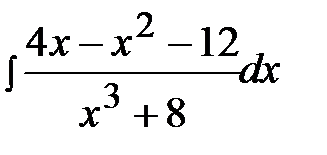 12.28
12.28 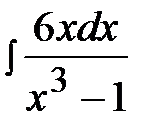
12.14. 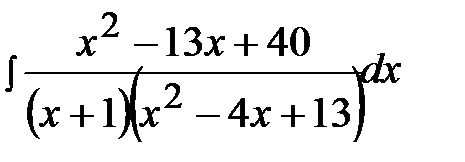 12.29.
12.29. 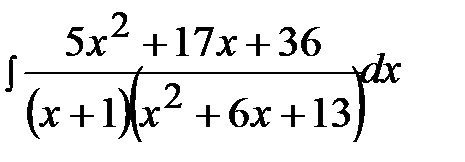
12.15. 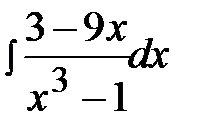 12.30.
12.30. 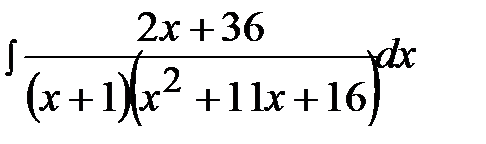
Пример 13.
13.1 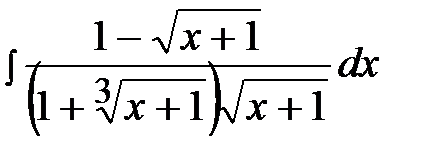 13.16
13.16 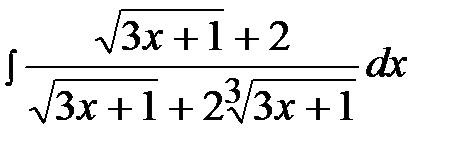
13.2 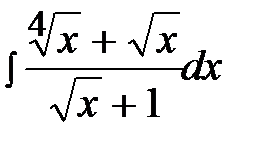 13.17
13.17 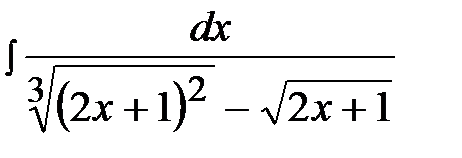
13.3 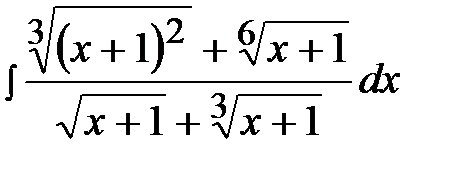 13.18
13.18 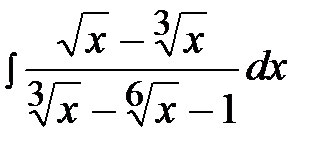
13.4 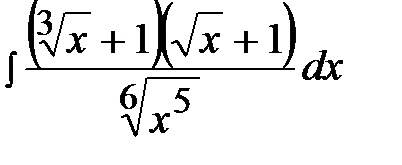 13.19
13.19 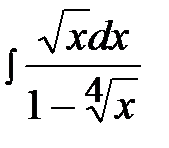
13.5 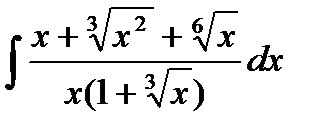 13.20
13.20 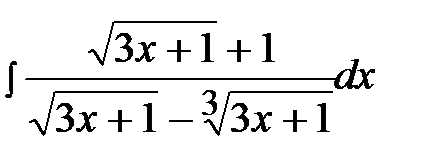
13.6 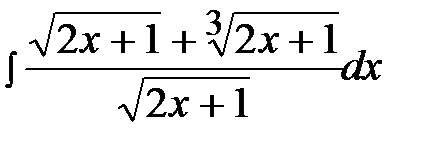 13.21
13.21 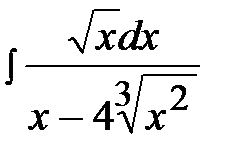
13.7 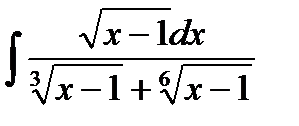 13.22
13.22 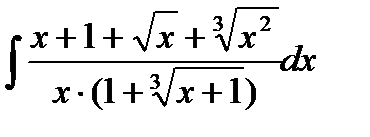
13.8 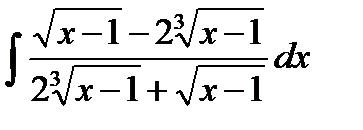 13.23
13.23 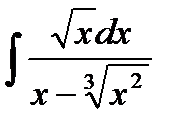
13.9 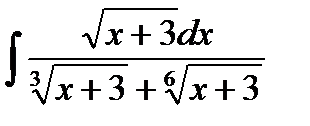 13.24
13.24 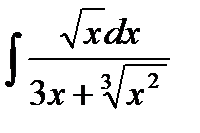
13.10 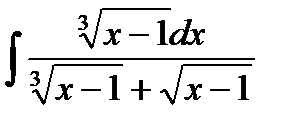 13.25.
13.25. 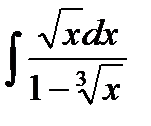
13.11 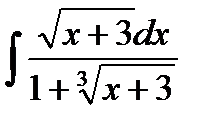 13.26
13.26 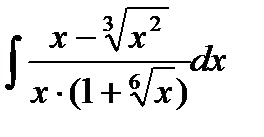
13.12 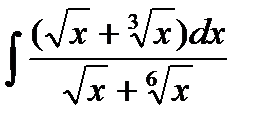 13.27
13.27 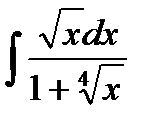
13.13 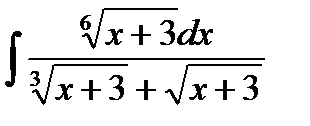 13.28
13.28 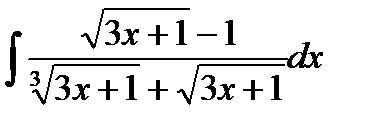
13.14 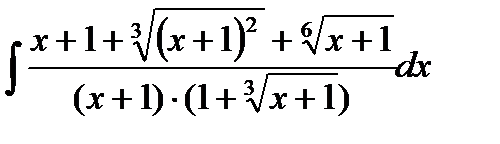 13.29
13.29 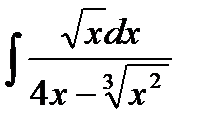
13.15 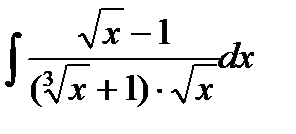 13.30
13.30 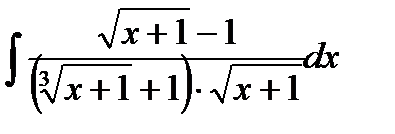
Пример 14.
14.1. 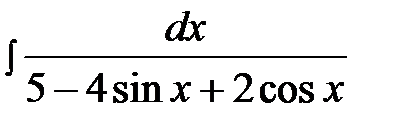 14.16.
14.16. 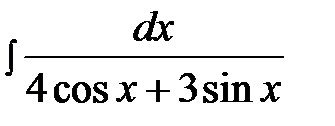
14.2. 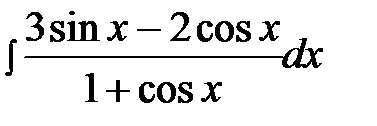 14.17.
14.17. 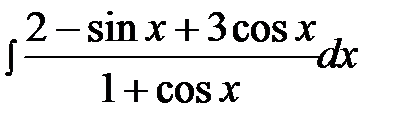
14.3. 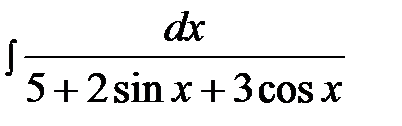 14.18.
14.18. 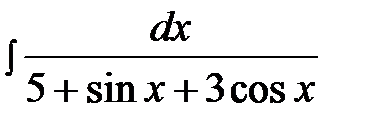
14.4. 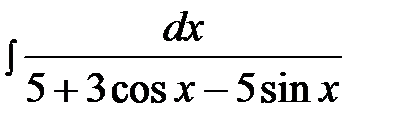 14.19.
14.19. 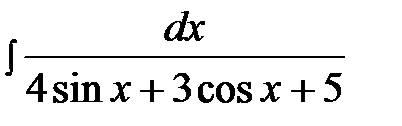
14.5. 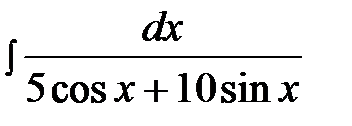 14.20.
14.20. 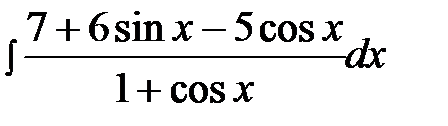
14.6. 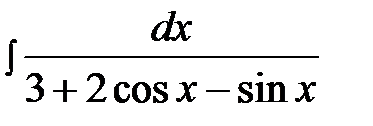 14.21.
14.21. 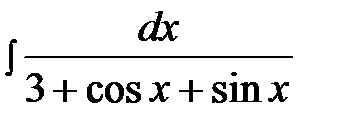
14.7. 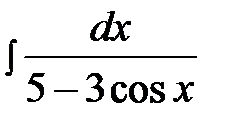 14.22.
14.22. 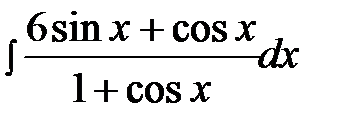
14.8. 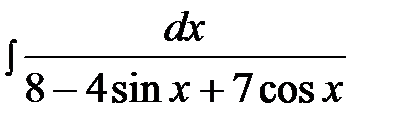 14.23.
14.23. 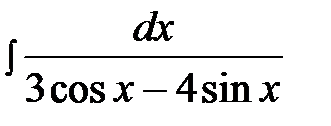
14.9. 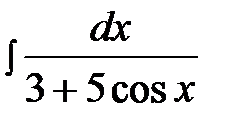 14.24.
14.24. 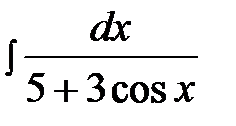
14.10. 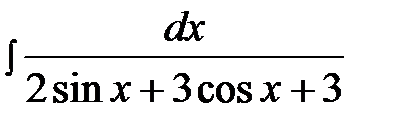 14.25.
14.25. 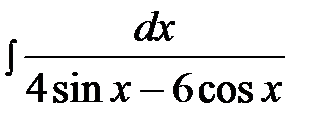
14.11. 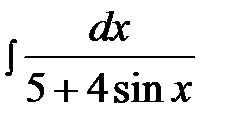 14.26.
14.26. 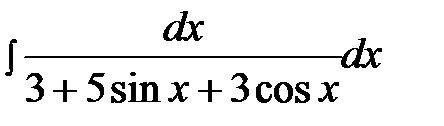
14.12. 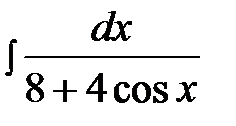 14.27.
14.27. 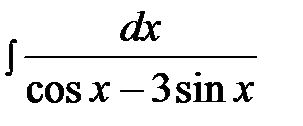
14.13. 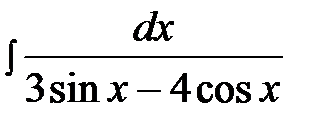 14.28.
14.28. 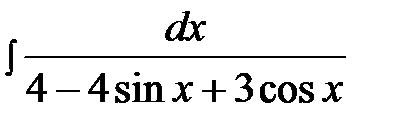
14.14. 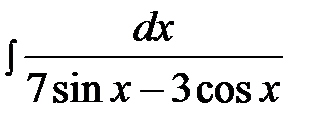 14.29.
14.29. 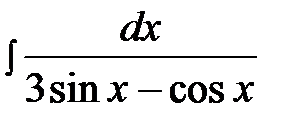
14.15. 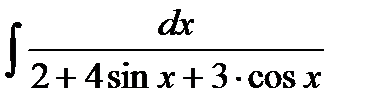 14.30.
14.30. 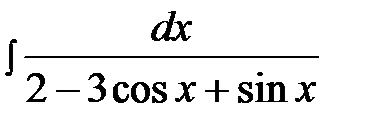
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Письменный Д. Т.
Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - 9-е изд. - М.: Айрис-Пресс, 2008. – 280 с.- Ч. 1.
2. Пискунов Н. С.
Дифференциальное и интегральное исчисления: учеб. пособие для вузов / Н. С. Пискунов. - изд. стер.. - М.: Интеграл-Пресс, 2006. – 415 с. Т.1.
3. Шипачев В.С.
Курс высшей математики: учебник для вузов / В.С.Шипачев; Под редакцией А.Н. Тихонова. – 3-е изд., испр. – М.: Издательство Оникс, 2007 – 600 с.: ил.
4. Берман Г. Н.
Сборник задач по курсу математического анализа: учеб. пособие / Г. Н. Берман. - 22-е изд., перераб. - СПб.: Профессия, 2006 - 432 с.
5. Лунгу К.Н.
Сборник задач по высшей математике: учеб. пособие / К.Н.Лунгу и др.- 7-е изд..- М.: Айрис Пресс, 2008.- 574 с.
6. Шипачев В. С.
Задачник по высшей математике: учеб. пособие для вузов / В. С. Шипачев. - 8-е изд., стер. - М.: Высш. шк., 2008. - 304 с.: ил.
7. Данко П. Е.
Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд.. - М.: ОНИКС.- 2008.-368 с.- Ч.1.
 2015-04-20
2015-04-20 579
579







