2015-04-20
5071
Рассмотрим интегралы следующих видов:
; 
;
; 
.
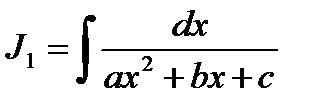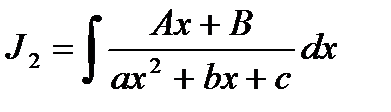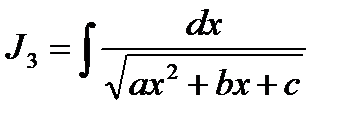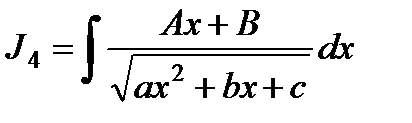Мы увидим в дальнейшем, что без умения находить такие интегралы, мы не сможем вычислять интегралы от рациональных дробей.
Сначала научимся находить более простые интегралы видов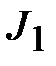 
и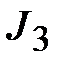 
.
Трудность заключается в наличии слагаемого bx. Если бы его не было, то, вынося за знак интеграла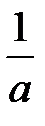 
, получили бы интеграл вида (11) или (12). Решить проблему можно выделением полного квадрата.
Пример 21.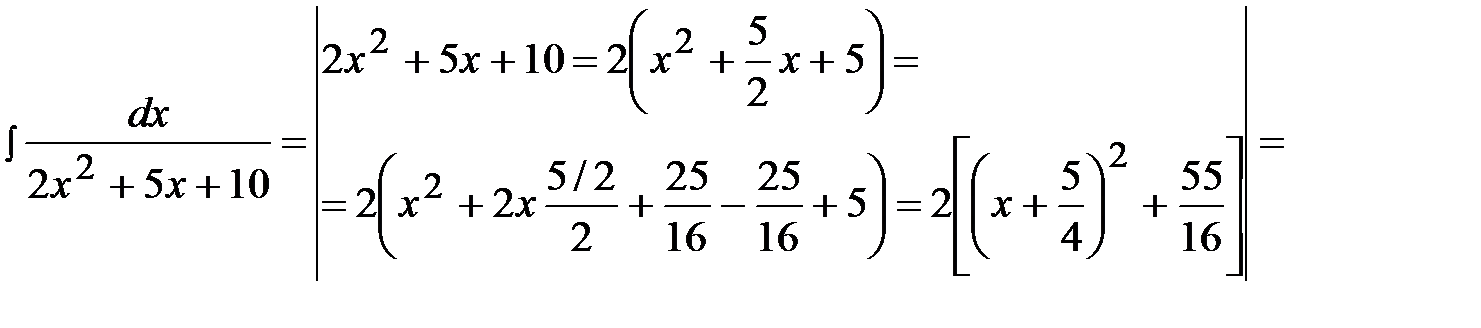 
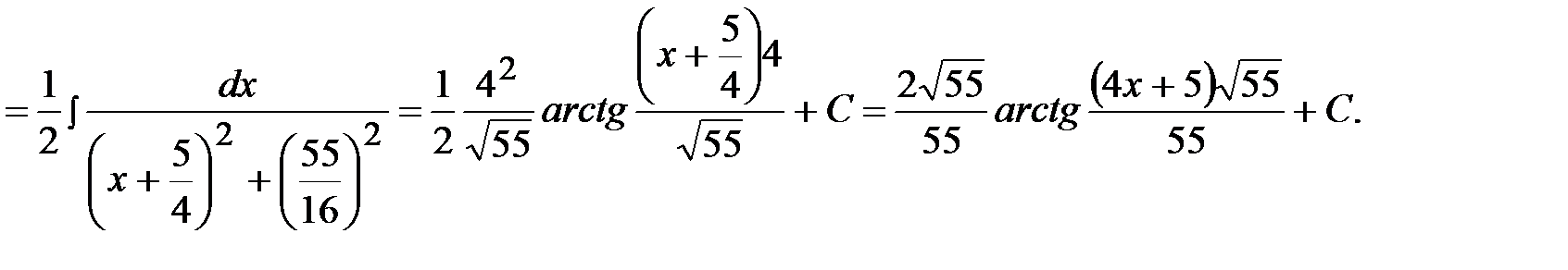Пример 22.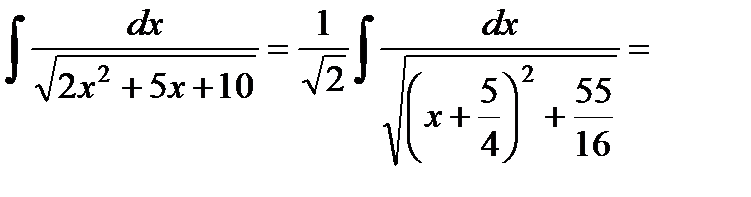 
.
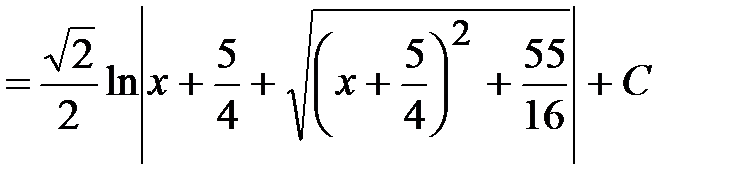Пример 23.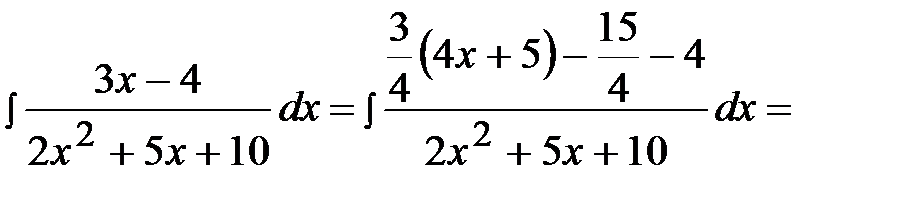 
.
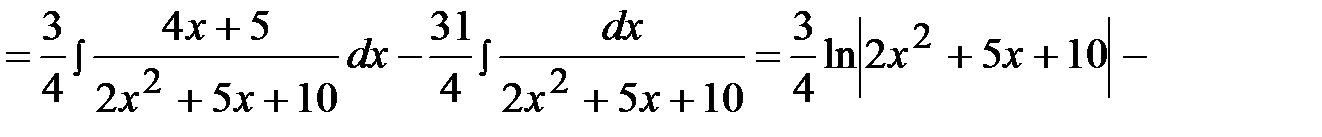
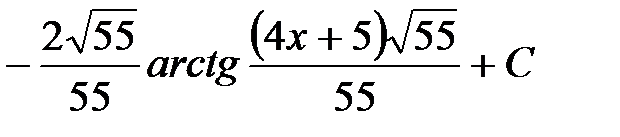По той же схеме находятся интегралы вида
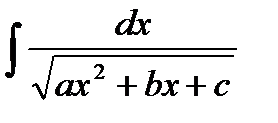и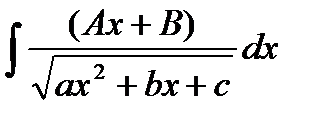 
С помощью таких же действий, что и в предыдущих случаях, указанные интегралы сводятся к табличным. При этом в первом случае возникают табличные интегралы вида:
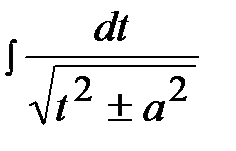и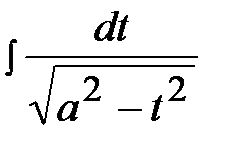 
.
Пример 24.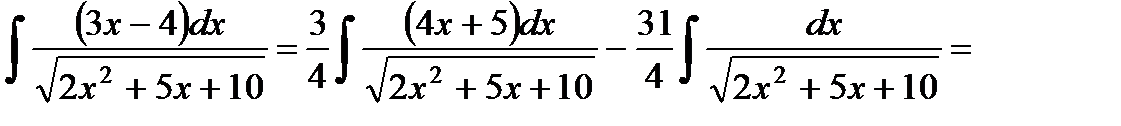 
.
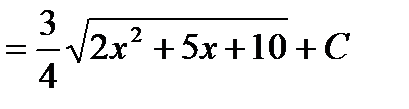1. Какие виды интегралов, содержащие квадратный трехчлен в знаменателе, вы знаете?
2. К каким табличным интегралам сводятся после выделения полного квадрата интегралы вида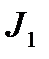 
и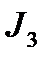 
?
3. По какому принципу интегралы вида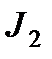 
и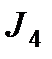 
разбиваются на два интеграла?
