Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
Если итоговая число по формуле получится больше 20, то для определения варианта от полученного числа отнимают 20.
Пример.
Пусть шифр студента 1298.
Номер варианта второго задания: 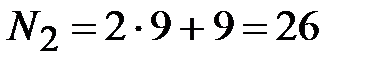 . Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
. Промежуток 26-20=6. Таким образом, во втором задании студент решает задачу варианта №6.
Первообразная функции и неопределенный интеграл
Функция 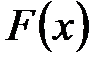 называется первообразной функции
называется первообразной функции 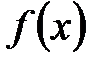 , если
, если
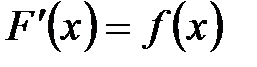 .
.
Другими словами, задача нахождения первообразной равносильна
восстановлению функции 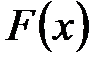 по ее производной
по ее производной 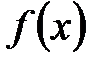 .
.
Например, для функции 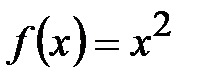 , первообразная -
, первообразная - 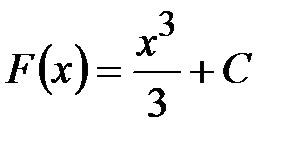 .
.
Как видим, первообразная определяется не единственным образом, а
с точностью до постоянного слагаемого.
Вообще говоря, не любая функция имеет первообразную. Можно доказать, что любая непрерывная функция имеет первообразную, то есть непрерывность является достаточным условием существования первообразной для заданной функции.
Множество всех первообразных функции функций 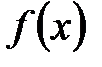 называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 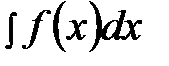 , таким образом:
, таким образом:
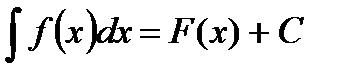 ,
, 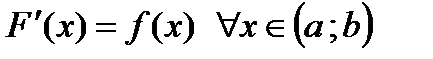 .
.
Отметим, что операции дифференцирования и интегрирования взаимнообратны в следующем смысле:
1) 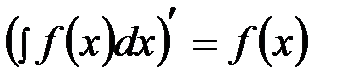 ,
,
2)  .
.
Таблица интегралов
1) 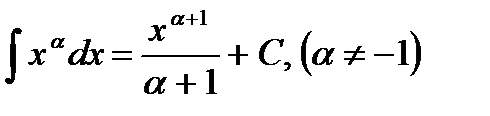 7)
7) 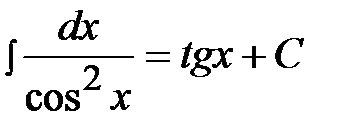 ,
,
2) 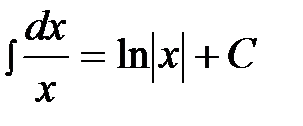 , 8)
, 8) 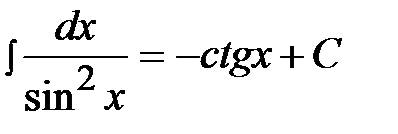 ,
,
3) 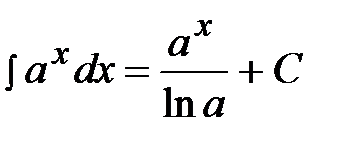 , 9)
, 9) 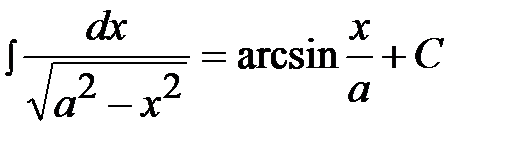 ,
,
4) 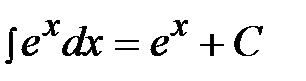 , 10)
, 10) 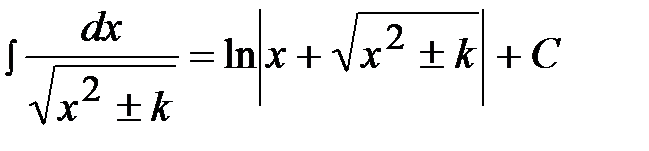 ,
,
5) 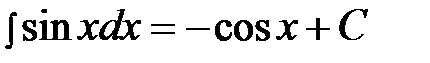 , 11)
, 11) 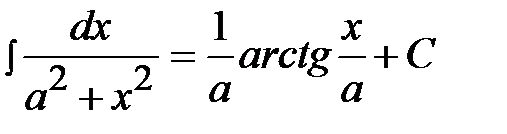 ,
,
6) 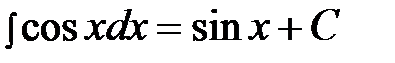 , 12)
, 12) 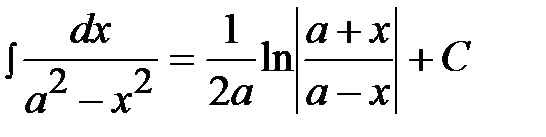 .
.
Нетрудно заметить, что большинство формул таблицы получено из таблицы производных.
Примеры применения формулы 1):
Пример 1. 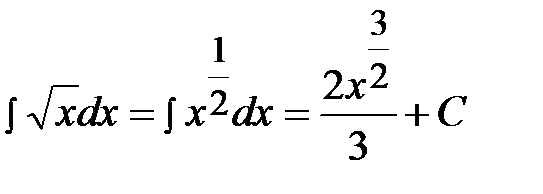 .
.
Пример 2. 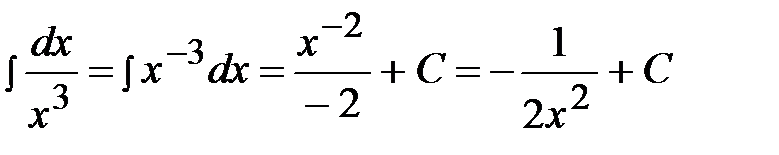 .
.
Пример 3. 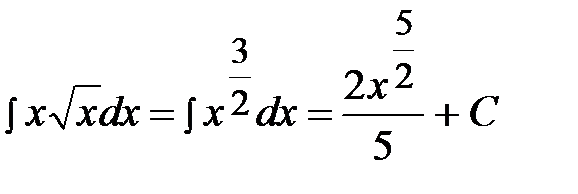 .
.
Пример 4. 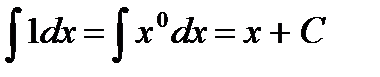 .
.
Как мы увидим в дальнейшем, особую роль при вычислении интегралов играют формулы 9) – 12). Рассмотрим примеры их применения:
Пример 5. 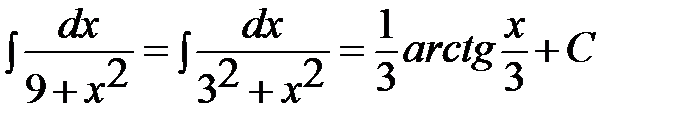 .
.
Пример 6. 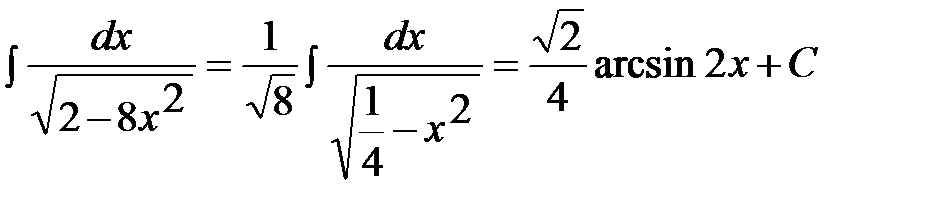 .
.
Пример 7. 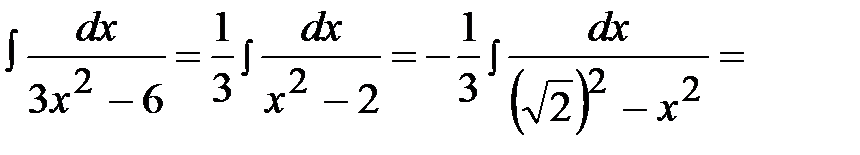
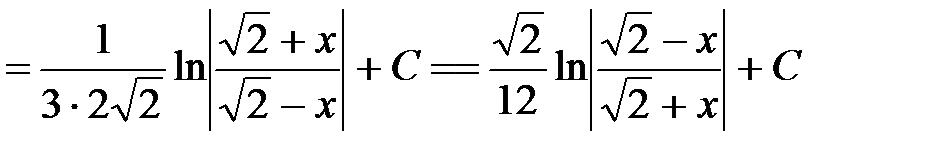 .
.
 2015-04-20
2015-04-20 548
548







