Методы подстановки и замены переменного

Пусть требуется найти неопределенный интеграл от непрерывной функции 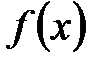на интервале (a;b).

Рассмотрим некоторую функцию 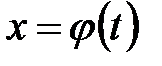, которая имеет непрерывную производную 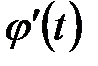и обратную функцию 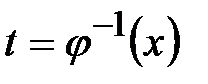. (Например: 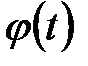монотонна). Тогда справедлива формула:

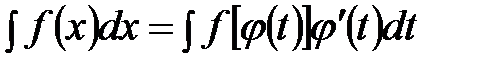. (2.1)

В некоторых ситуациях удается подобрать функцию 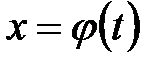так, что интеграл в правой части (1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:

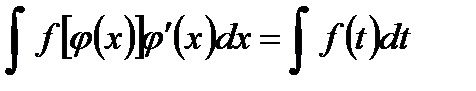(2.1)

Другими словами, если подынтегральное выражение может быть записано в форме левой части (2.1), то с помощью подстановки 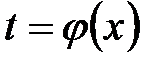получаем более простой интеграл.

Пример 8. .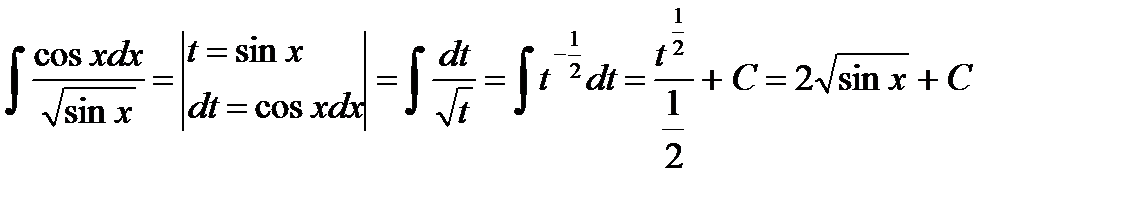

Пример 9.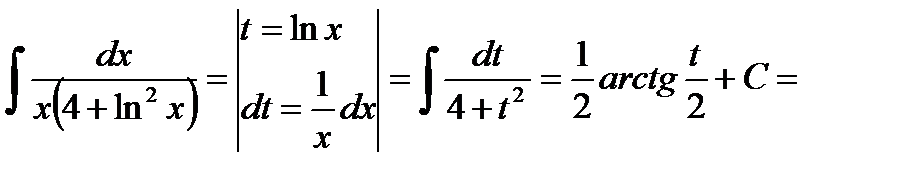

.

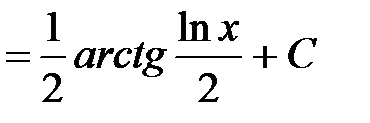Правильность вычисления интеграла можно проверить: производная найденного интеграла должна совпадать с подынтегральной функцией. В нашем примере:

.

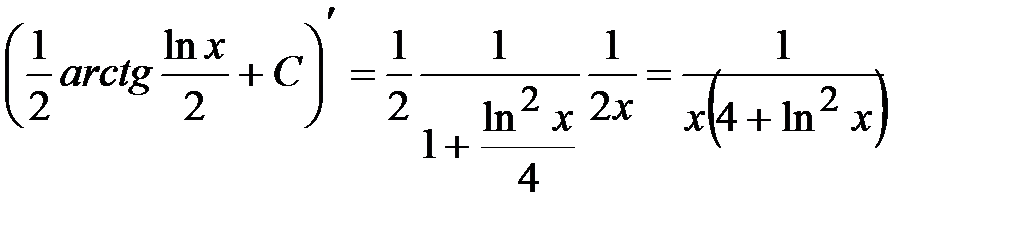Пример 10. .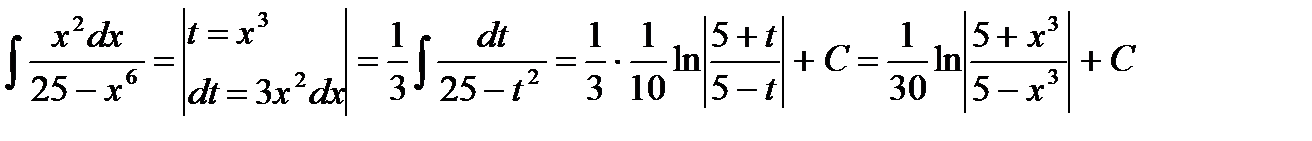

Пример 11. .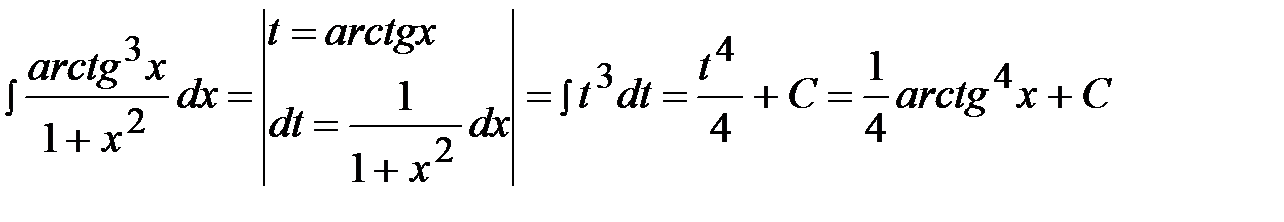

На практике часто используется следующая простая формула:

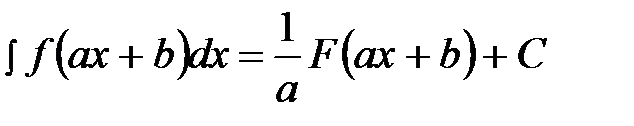, (2.2)

где 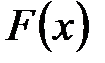- первообразная для функции .

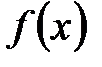Пример 12. .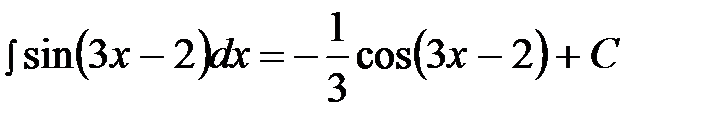

Пример 13. .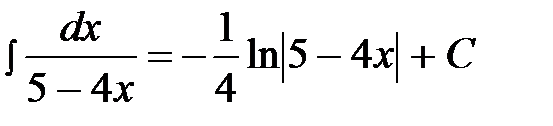

Пример 14. .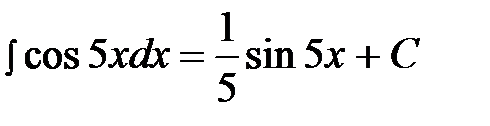

Вопросы для самопроверки

1. Что называется первообразной функции ?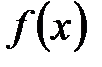

2. Что означает произвольная постоянная интегрирования С?

3. В чем заключается основная идея метода замены переменной?

4. Каким условиям должна удовлетворять функция 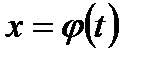при замене переменной?