Решите транспортную задачу по имеющимся данным (в левых верхних углах клеток таблицы указаны стоимости перевозок единицы сырья соответствующему потребителю).
Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2 и А3 находится груз соответственно в количестве а1, а2 и а3 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно b1, b2, b3, b4 и b5 тонн груза. Расстояние между пунктами поставки и пунктами потребления приведено в следующей матрице- таблице:
| Пункты поставки | Пункты потребления | ||||
| В1 | В2 | В3 | В4 | В5 | |
| А1 | d11 | d12 | d13 | d14 | d15 |
| А2 | d21 | d22 | d23 | d24 | d25 |
| А3 | d31 | d32 | d33 | d34 | d35 |
Найти план закрепления потребителей за поставщиками однородного груза, чтобы общие затраты по перевозкам были минимальными. Составить математическую модель задачи и решить ее, используя поиск решения таблиц EXCEL
а1=150
а2=150
а3=200
b1 =100; b2 =70; b3 =130; b4 =110; b5=90
D = 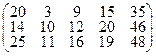
Решение
Найдем сумму запасов и сумму потребностей: a1+a2+a3=150+150+200=800; b1+b2+b3+b4+b5=100+70+130+110+90=500
Сумма запасов равна сумме потребностей, то есть все запасы должны быть вывезены, и все потребности удовлетворены.
Обозначим xi,j–количество груза перевозимого от Ai к Bj и составим математическую модель задачи.
Целевая функция – общие затраты на перевозки
Z=20x11+3x12+9x13+15x14+35x15+
+14x21+10x22+12x23+20x24+46x25+
+ 25x31+11x32+16x33+19x34+48x35→min.
Ограничения:
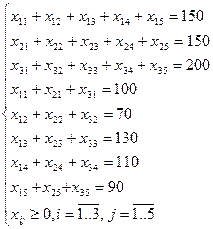
Найти неотрицательные значения xi,j удовлетворяющие системе ограничений и минимизировать функцию z – затраты по перевозке.
Выполним последовательность действий для решения задачи, используя модуль Поиск решения.
1. Записываем все данные в таблицу.
· В ячейку В2:Н2 запишем Транспортная задача
· В ячейку В3:G3 запишем Тарифы
· В ячейку Н3: Запасы
· Записываем в ячейку A7: Потребности
· В ячейки С4:G6 записываем матрицу перевозок D
· В ячейку В8:G8 запишем План перевозок
· Заносим 0 в блок ячеек B9:F11
В ячейку В12: F12 запишем Общие затраты -целевая функция
· В ячейку C13: Целевая функция
2. Записываем в ячейку B13 формулу =СУММПРОИЗВ(C4:G6;B9:F11)
3. В ячейку H4 записываем формулу =СУММ(B9:F9) и копируем ее в ячейки H5 и H6
4. В ячейку H7 записываем формулу =СУММ(B9:F9) и копируем ее в ячейки I7,J7,K7 и L7
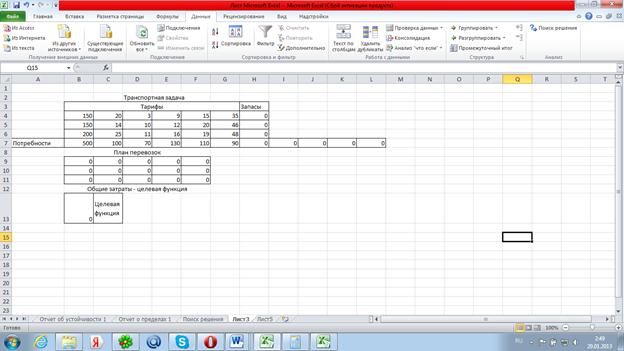
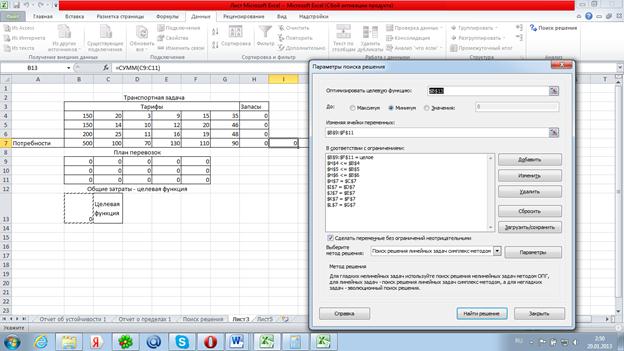
5. Далее в Сервис-Поиск решения берем целевую функцию, min,поле для значений и ограничения, как показано на рисунке.
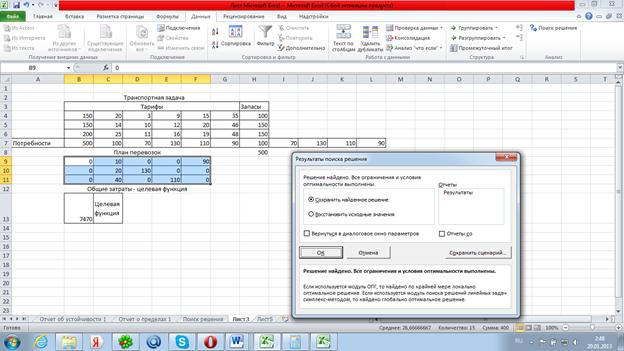
| Транспортная задача | |||||||||||
| Тарифы | Запасы | ||||||||||
| Потребности | |||||||||||
| План перевозок | |||||||||||
| Общие затраты - целевая функция | |||||||||||
| Целевая функция |
Используемая литература:
1. Л.П. Бойченко, О.Н. Туманова. Экономико-математические методы и модели: Учебное пособие. – Ухта: УГТУ, 1999. – 125 с., ил.
2. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. – 391 с.
 2015-04-20
2015-04-20 11873
11873







