1. Определяем число групп по таблице 2.1 (тема 2):
при N=45 число групп (g) соответствует 6.
2. Рассчитываем интервал:
| Δх = | xmax - xmin | = | 18 – 1 | = 2, 83 ≈ 3 |
| g |
3. Определяем моду (Мо): наиболее часто встречается варианта со значением 8. Значит, Мо = 8.
Достаточно часто Мо равна условной средней (А). Значит, Мо = А = 8.
4. Составляем сгруппированный вариационный ряд, находим середины групп, частоту их встречаемости, условное отклонение в интервалах и его произведение на частоту. Ранее аналогичные расчеты приводились в теме 2.
| Длительность нахождения на бюллетене | Середина группы (с) | Частота встречаемости вариант интервала (n) | Условное отклонение (аi) аi = (с – А)/ Δx | аi ni | аi2 ni |
| 1-3 | (2-8)/3 = -2 | (-2)*4 = -8 | (-2)2*4=16 | ||
| 4-6 | (5-8)/3 = -1 | (-1)*9 = -9 | (-1)2*9=9 | ||
| 7-9 | (8-8)/3 = 0 | 0*15 = 0 | 0*15=0 | ||
| 10-12 | (11-8)/3 = 1 | 1*8 =8 | 12*8=8 | ||
| 13-15 | (14-8)/3 = 2 | 2*6=12 | 22*6=24 | ||
| 16-18 | (17-8)/3 = 3 | 3*3=9 | 32*3=27 |
N = 45; k k
∑ аi ni = 12; ∑ аi2 ni = 84
i=1 i=1
5. Определяем взвешенную среднюю арифметическую по способу моментов:
| Xв = A + | k ∑ аi ni i=1 | * Δx = 8 + | * 3 = 8,8 | |
| N |
6. Находим среднее квадратическое отклонение:
| S = Δx * | √ | N ∑ аi2ni i=1 | – | ( | N ∑ аini i=1 | ) | 2 | = | |
| N | N |
| = 3* | √ | - | ( | ) | 2 | = 4,02 | ||
7. Рассчитываем стандартную ошибку среднего арифметического:
| при N >30 | |
| µ`x = | S | = | 4,02 | = 0,6 |
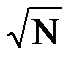
| 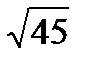
|
8. Находим доверительный интервал с учетом того, что при
| α = 0,05 (5%) | ⇒ | γ = 95% | } | Т= ε95 = 1,96 ≈ 2 |
| α = 0,01 (1%) | ⇒ | γ = 99% | Т= ε99 = 2,7 ≈ 3 |
∆ = ε95 *µ = 2 ∙ 0,6 = 1,2
Таким образом, доверительные интервалы средней величины (`x -Δ и `x +Δ) с вероятностью 95%: X = 8,8 + 1,2 или средняя длительность нахождения на бюллетене от 7,6 до 10,0 или от 8 до 10 дней.
∆ = ε99 *µ = 3 ∙ 0,6 = 1,8
Значит, доверительные интервалы средней величины (X-Δ и X+Δ) с вероятностью 99%: X = 8,8 + 1,8 или средняя длительность нахождения на бюллетене от 7,0 до 10,6 или от 7 до 11 дней.
 2015-04-20
2015-04-20 412
412








