Обозначим через 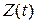 количество продуктов одной группы товаров на складе в момент времени
количество продуктов одной группы товаров на складе в момент времени 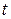 . Предположим, что спрос на эту товарную группу на период времени
. Предположим, что спрос на эту товарную группу на период времени 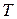 представляет собой детерминированную величину, то есть продажа товаров в единицу времени осуществляется равномерно с известной интенсивностью
представляет собой детерминированную величину, то есть продажа товаров в единицу времени осуществляется равномерно с известной интенсивностью 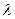 руб./день.
руб./день.
С течением времени товарные запасы уменьшаются и, достигнув определенного уровня 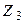 в момент времени
в момент времени 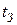 , называемый точкой заказа, сигнализируют о необходимости подачи заказа величиной
, называемый точкой заказа, сигнализируют о необходимости подачи заказа величиной 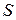 на пополнение запасов (рис.7.1).
на пополнение запасов (рис.7.1).
 |
Рис.7.1. Динамика изменения товарных запасов
Полагая, что время на выполнение заявки известно и равно 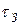 , поступление (и прием) товара на склад произойдет в момент времени
, поступление (и прием) товара на склад произойдет в момент времени 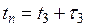 , когда на складе останется лишь страховой запас
, когда на складе останется лишь страховой запас 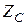 .
.
Пусть в начальный момент времени 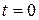 объем товарных запасов составлял величину
объем товарных запасов составлял величину 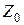 , а продажа товаров за время
, а продажа товаров за время 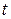 составляет
составляет 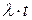 .
.
Время подачи заказа на пополнение запаса 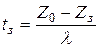 .
.
За время выполнения заказа 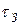 будет продано товаров
будет продано товаров 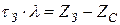 , тогда интервал поставок определяется уравнением
, тогда интервал поставок определяется уравнением
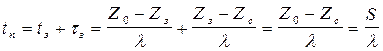 .
.
Число поставок за любой период 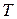 или на момент времени
или на момент времени 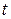 определяется выражением
определяется выражением 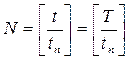 , где [...] - целая часть числа.
, где [...] - целая часть числа.
Общий объем поставок за период 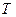 определится соотношением
определится соотношением
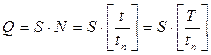 .
.
Таким образом, уровень товарных запасов на любой момент времени 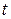 определяется уравнением
определяется уравнением 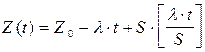 .
.
Систему хранения товарных запасов можно интерпретировать в виде балансовой формулы: 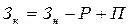 ,
,
где 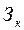 - запас на конец анализируемого периода времени (
- запас на конец анализируемого периода времени (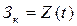 );
);
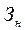 - запас на начало периода (
- запас на начало периода (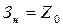 );
);
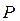 - реализация, объем товарооборота (
- реализация, объем товарооборота (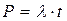 );
);
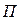 - поступление товаров (
- поступление товаров (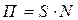 ).
).
Задача управления товарными запасами состоит в выборе оптимальной величины заказов (поставки) товаров 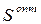 , интервала между поставками
, интервала между поставками 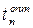 , числа поставок
, числа поставок 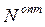 за период
за период 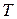 и среднего запаса
и среднего запаса 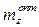 .
.
Критерием оптимальности могут служить суммарные издержки С по управлению товарными запасами:
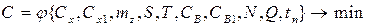 ,
,
где 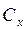 - затраты на хранение товаров за период
- затраты на хранение товаров за период 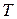 ;
;
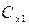 - затраты на хранение единицы товара в течение года;
- затраты на хранение единицы товара в течение года;
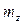 - величина среднего запаса
- величина среднего запаса 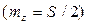 ;
;
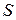 - размер одной партии поставки товара;
- размер одной партии поставки товара;
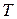 - величина анализируемого периода (лет);
- величина анализируемого периода (лет);
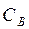 - затраты на транспортировку (завоз, ввоз);
- затраты на транспортировку (завоз, ввоз);
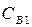 - затраты на ввоз (завоз) одной партии товара;
- затраты на ввоз (завоз) одной партии товара;
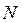 - число поставок за анализируемый период
- число поставок за анализируемый период 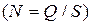 ;
;
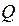 - общий объем поставок за анализируемый период Т;
- общий объем поставок за анализируемый период Т;
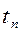 - интервал поставок.
- интервал поставок.
В частности, критерий минимизации издержек обращения запишется в виде:
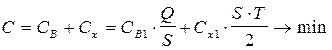 .
.
Исходными данными для решения задачи (неуправляемыми параметрами в целевой функции) являются величины 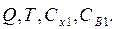
Остальные параметры - управляемые. Их оптимальные значения 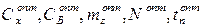 обеспечивают минимум издержек обращения.
обеспечивают минимум издержек обращения.
Для нахождения оптимальных величин этих параметров определяем экстремум целевой функции 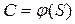 путем дифференцирования по
путем дифференцирования по 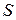 и приравнивания производной к нулю:
и приравнивания производной к нулю:
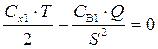 .
.
Отсюда получаем модели расчета оптимальных параметров системы управления однономенклатурными запасами (рис.7.2):
1) размер одной поставки товаров: 
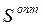
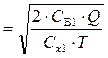 ;
;
2) средний запас текущего хранения: 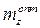
 /2;
/2;
3) число поставок за период 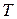 :
: 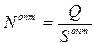 ;
;
4) интервал между поставками: 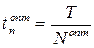 ;
;
5) величина минимальных издержек: 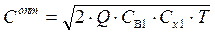 .
.
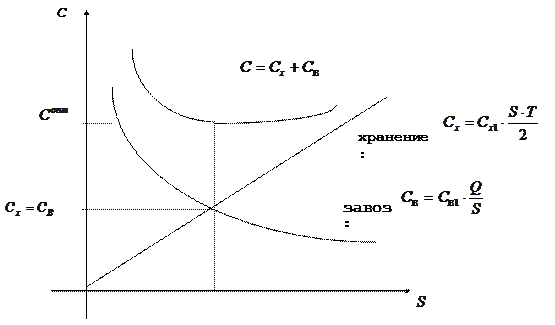 |
Рис.7.2. Зависимость издержек от размера партии поставки
Механизм управления товарными запасами разных групп товаров сложнее, поэтому при моделировании обычно идут по пути упрощения и модификации детерминированных моделей управления запасами по одной товарной группе.
Основу модификации составляет предположение о том, что отношение затрат на завоз партии товара к затратам на хранение единицы товара по всем  товарным группам одинаково.
товарным группам одинаково.
На этом основании можно модель оптимального числа поставок преобразовать в такой вид:
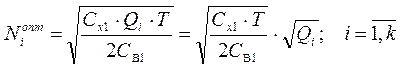 .
.
Обозначив выражение 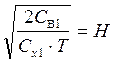 , получим модель расчета оптимальных параметров товароснабжения для каждой товарной группы:
, получим модель расчета оптимальных параметров товароснабжения для каждой товарной группы:
1) размер одной партии товаров: 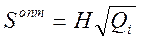 ;
;
2) средний запас текущего хранения: 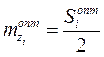 ;
;
3) число поставок: 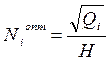 ;
;
4) интервал между поставками: 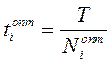 .
.
Необходимую для расчетов величину 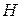 можно определить из предположения, что эта величина одинакова по всем товарным группам, по соотношению:
можно определить из предположения, что эта величина одинакова по всем товарным группам, по соотношению:
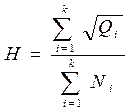 .
.
 2015-04-23
2015-04-23 1022
1022
