Температурным полем называется совокупность значений температуры в каждый момент времени во всех точках рассматриваемого пространства. Если температура постоянна во времени, то поле называется стационарным или установившимся. Если же температура во времени меняется, то поле называется нестационарным (неустановившимся).
Температура может быть функцией трёх, двух и одной координат. В соответствии с этим различают трёх-, двух-, и одномерные температурные поля.
Математически нестационарное трёхмерное температурное поле, в общем случае задаётся уравнением, связывающим значение температуры в каждой точке тела со значением координат этой точки в данный момент времени и имеет вид[1]:
t = t (x, y, z, τ), (9.1)
где τ – время;
а стационарного поля:
t = t (x, y, z). (9.2)
Поверхности, представляющие собой геометрическое место точек с одинаковой температурой, называют изотермическими поверхностями, а линии пересечения изотермической поверхности с плоскостью – изотермами (рис. 9.1.).
В окрестности данной точки температура изменяется во всех направлениях, не совпадающих с касательной к изотерме. При этом наиболее резкое изменение температуры имеет место в направлении по нормали к изотермической поверхности.
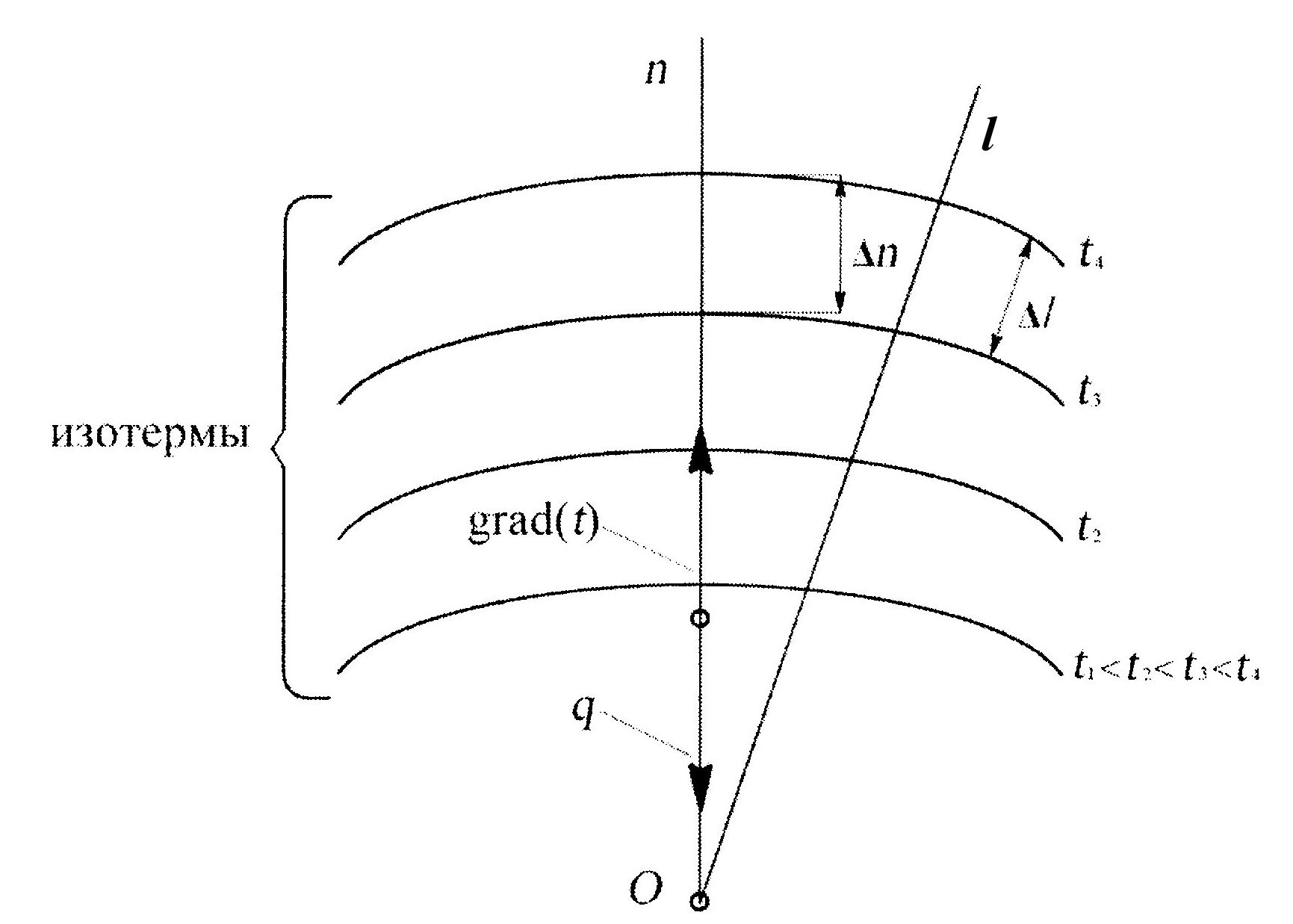
Рис. 9.1. Температурное поле. Удельный тепловой поток, градиент температуры
Градиент температуры. Производная температуры по нормали к изотермической поверхности называется градиентом температуры:
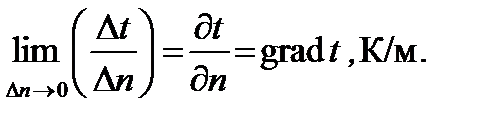 (9.3)
(9.3)
Эта величина является вектором, направленным по нормали к изотермической поверхности в сторону увеличения температуры (см. рис. 9.1.).
Градиент температуры характеризует интенсивность изменения температуры в направлении нормали. Интенсивность изменения температуры в произвольном направлении меньшая, чем в направлении нормали, и равна проекции на это направление:
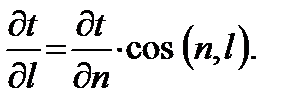
 2015-04-23
2015-04-23 12207
12207
