Дифференциальное уравнение теплопроводности

Одной из основных задач теории теплообмена является определение температурного поля, т.е. пространственно-временного распределения температуры в исследуемой области. Это распределение подчиняется дифференциальному уравнению теплопроводности, которое вытекает из закона сохранения и превращения энергии.

Вначале рассмотрим однородное тело, температура которого меняется только в направлении х.

Будем считать, что в теле отсутствуют внутренние источники тепла, а физические свойства не зависят от температуры. Выделим в этом теле (рис. 9.3.) объем толщиной dx;площадь поверхностей граней, перпендикулярных оси х,равна F. За время dτ в этот объём поступает тепло dQ _х;а выходит из него dQ _х+dx. Тогда:

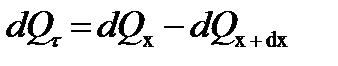(9.8)

где dQ _τ – количество тепла, аккумулированного телом и пошедшего на изменение его температуры.

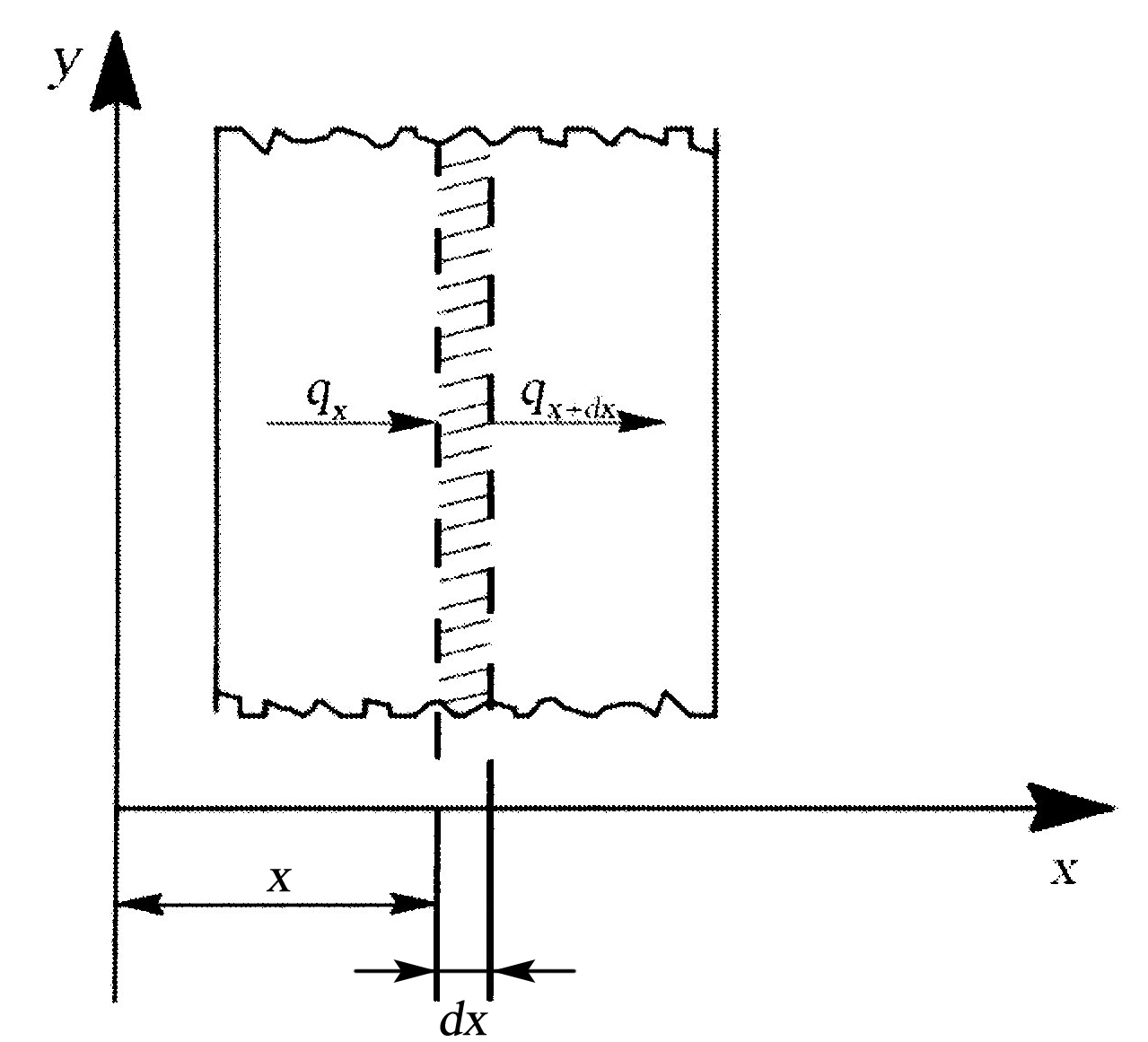
Рис. 9.3. К выводу уравнения теплопроводности

Нетрудно видеть, что:

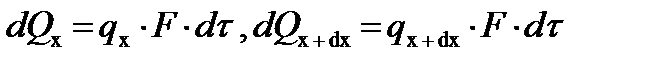(9.9)

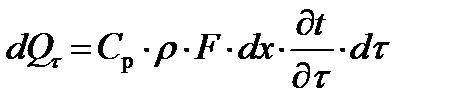(9.10)

Здесь q _х и q _{х + d x} – плотности теплового потока в плоскостях х и dх,причём:

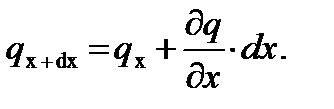(9.11)

Из закона Фурье (9.6) следует (при λ = const):

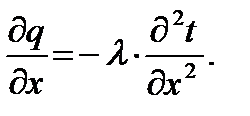(9.12)

Тогда:

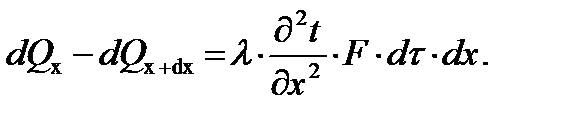(9.13)

Подставляя (9.10) и (9.13) в (9.8), получим:

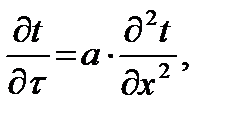(9.14)

где

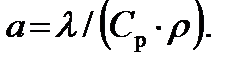
Уравнение (9.14) является дифференциальным уравнением теплопроводности для одномерного температурного поля. В общем случае трёхмерного поля уравнение имеет вид:

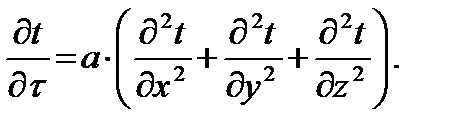(9.15)

Дифференциальное уравнение теплопроводности устанавливает связь между временным и пространственным изменением температуры в любой точке тела, в котором происходит перенос тепла теплопроводностью. Комплекс а называется коэффициентом температуропроводности. Как и величины, из которых составлен комплекс, коэффициент температуропроводности является физическим параметром вещества.

Из уравнений (9.14) и (9.15) видно, что скорость изменения температуры 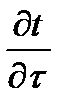в любой точке тела тем выше, чем больше величина а. Поэтому можно считать, что коэффициент температуропроводности является мерой теплоинерционных свойств материала.

Дифференциальное уравнение теплопроводности получено на основе самых общих представлений о процессе и поэтому справедливо для всех без исключения процессов теплопроводности, протекающих без внутренних источников тепла. Чтобы получить решение, соответствующее конкретной задаче, надо к этому уравнению присовокупить математическое описание частных особенностей данного процесса. Эти частные особенности называются краевыми условиями. Они включают в себя временные и граничные условия.

Временные условия определяют температурное поле в изучаемом теле в какой-либо момент времени; поэтому часто временные условия называются начальными.

Граничные условия определяют значения переменных на границах пространства и в данном случае состоят в задании распределения температуры тела на его поверхности в функции времени или задании условий теплового взаимодействия тела с окружающей средой.