При вычислении значения функции 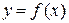 в точке
в точке 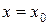 (считаем
(считаем 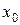 приближенным значением точного числа
приближенным значением точного числа 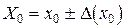 ) возникают погрешности – предельная абсолютная
) возникают погрешности – предельная абсолютная 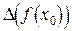 и предельная относительная
и предельная относительная 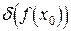 . Выразим эти погрешности через погрешности числа
. Выразим эти погрешности через погрешности числа 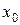 (будем полагать, что функция
(будем полагать, что функция 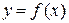 дифференцируема в точке
дифференцируема в точке 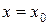 ).
).
Так как функция 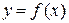 дифференцируема в точке
дифференцируема в точке 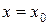 , то
, то
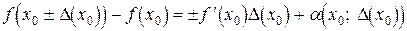 , (4.1)
, (4.1)
где 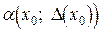 мало при малом
мало при малом 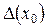 (иными словами, слагаемым
(иными словами, слагаемым 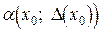 в формуле (4.1) можно пренебречь, если
в формуле (4.1) можно пренебречь, если 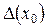 мало).
мало).
Учитывая равенство (4.1), истинная абсолютная погрешность 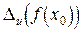 будет оцениваться неравенством (приближенным)
будет оцениваться неравенством (приближенным)
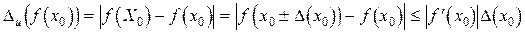 ,
,
откуда по определению предельной абсолютной погрешности
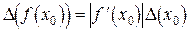 . (4.2)
. (4.2)
Итак, предельная абсолютная погрешность значения функции в точке 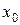 (
(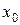 – приближенное число) равна произведению модуля производной этой функции в точке
– приближенное число) равна произведению модуля производной этой функции в точке 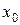 на предельную абсолютную погрешность числа
на предельную абсолютную погрешность числа 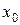 .
.
Соответственно предельная относительная погрешность 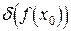 вычисляется следующим образом
вычисляется следующим образом
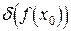 =
= 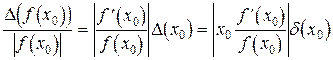 . (4.3)
. (4.3)
Найдем с помощью формул (4.2), (4.3) погрешности значений основных элементарных функций.
Пусть 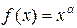 (
(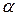 – действительное число). Тогда
– действительное число). Тогда
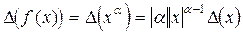 ,
, 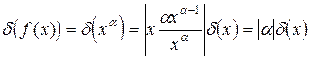 .
.
В частности при 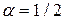 :
: 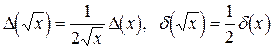 .
.
Пусть 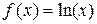 . Тогда
. Тогда
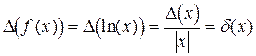 ,
, 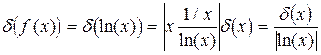 .
.
Пусть 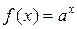 . Тогда
. Тогда
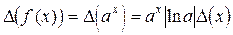 ,
, 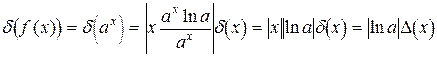 .
.
В частности, если 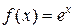 , то
, то 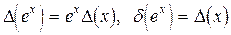 .
.
Аналогично определяются погрешности значений других основных элементарных функций (см. таблицу 4.1).
Таблица 4.1.
| № | 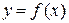
| 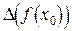
| 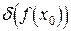
|
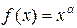
| 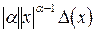
| 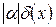
| |
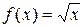
| 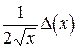
| 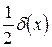
| |
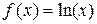
| 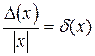
| 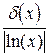
| |
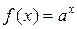
| 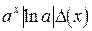
| 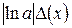
| |
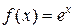
| 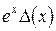
| 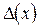
| |
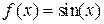
| 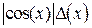
| 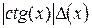
| |
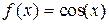
| 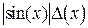
| 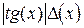
| |
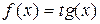
| 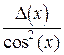
| 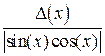
| |
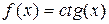
| 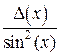
| 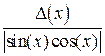
|
Пример 4.1. Дана функция 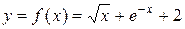 . Протабулировать ее на отрезке
. Протабулировать ее на отрезке 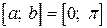 (считать
(считать 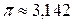 ), разбив его на
), разбив его на 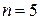 равных частей (все расчеты проводить с 4 знаками после запятой). Вычислить предельные абсолютные, относительные погрешности значений функции в узлах табулирования.
равных частей (все расчеты проводить с 4 знаками после запятой). Вычислить предельные абсолютные, относительные погрешности значений функции в узлах табулирования.
Решение: Протабулировать функцию 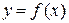 на отрезке
на отрезке 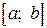 с постоянным шагом
с постоянным шагом 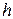 означает составить таблицу значений
означает составить таблицу значений 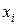 ,
, 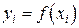 (точки
(точки 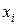 называются узлами табулирования), где
называются узлами табулирования), где
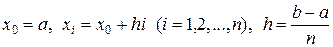 . (4.4)
. (4.4)
В нашем случае 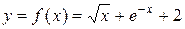 ,
, 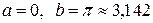 ,
, 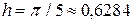 ; узлы определяются следующим образом:
; узлы определяются следующим образом:
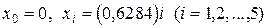 . (4.5)
. (4.5)
Вычислим значения функции в узлах табулирования (4.5):
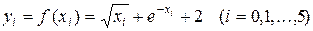 .
.
Имеем 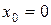 ,
, 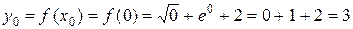 ;
;
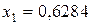 ,
, 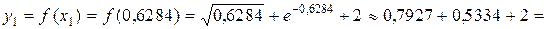 3,3261,
3,3261,
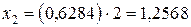 ,
, 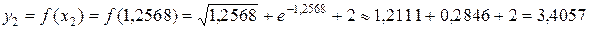
и так далее.
Все вычисления значения функции в узлах табулирования заполняем в таблицу 4.2.
Учитывая формулы (4.2), (4.3), находим погрешности в узлах (4.5) (при этом число 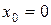 можно считать точным, а тогда
можно считать точным, а тогда 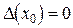 ; в остальных же узлах (4.5)
; в остальных же узлах (4.5) 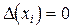 ,00005)
,00005)
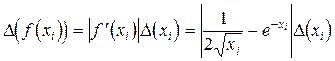 ,
, 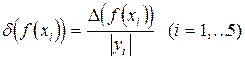 .
.
Таблица 4.2.
| i | 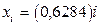
| 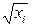
| 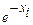
| 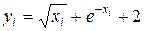
| 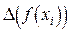
| 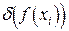
|
| 0,6284 | 0,7927 | 0,5334 | 3,3261 | 4,8678 
| 1,46 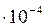
| |
| 1,2568 | 1,2111 | 0,2846 | 3,4057 | 8,0695 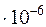
| 2,37 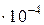
| |
| 1,8852 | 1,3730 | 0,1518 | 3,5248 | 1,0618 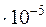
| 0,3 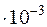
| |
| 2,5136 | 1,5854 | 0,0809 | 3,6663 | 1,1724 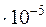
| 0,32 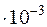
| |
| 3,1420 | 1,7726 | 0,0432 | 3,8158 | 1,1944 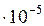
| 0,31 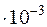
|
 2015-04-23
2015-04-23 1028
1028
