Всякое действительное число 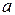 (десятичной системы счисления) можно записать в виде конечной или бесконечной десятичной дроби (в так называемой позиционной записи)
(десятичной системы счисления) можно записать в виде конечной или бесконечной десятичной дроби (в так называемой позиционной записи)
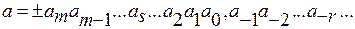 , (2.1)
, (2.1)
где 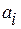 – десятичные цифры
– десятичные цифры
(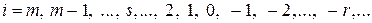 ),
),
причем 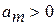 ; «
; «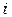 » – номер разряда, в котором стоит цифра
» – номер разряда, в котором стоит цифра 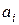 ;
;
разряд «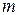 » называется старшим разрядом числа
» называется старшим разрядом числа 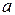 , разряд «
, разряд «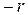 » – младшим разрядом (если дробь конечная) числа
» – младшим разрядом (если дробь конечная) числа 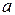 .
.
Единицей «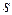 » -го разряда (разряда номера «
» -го разряда (разряда номера «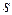 ») называется число
») называется число 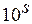 . Учитывая это, число
. Учитывая это, число 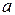 можно записать в виде позиционного разложения
можно записать в виде позиционного разложения
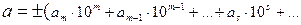
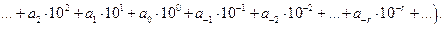 (2.2)
(2.2)
Пример 2.1. Число 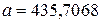 записать в виде позиционного разложения.
записать в виде позиционного разложения.
Решение: Имеем
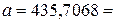
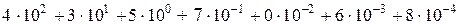 .
.
В таком разложении каждая цифра числа является множителем перед некоторой степенью десятки: цифра 4 стоит в разряде сотен (старший разряд «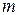 »=«2»). Следующая цифра 3 стоит в разряде десятков (разряд «1»), цифра 5 – в разряде единиц (разряд «0»), цифра 7 – в разряде десятых (разряд «–1») и так далее. Последняя цифра 8 стоит в младшем разряде «
»=«2»). Следующая цифра 3 стоит в разряде десятков (разряд «1»), цифра 5 – в разряде единиц (разряд «0»), цифра 7 – в разряде десятых (разряд «–1») и так далее. Последняя цифра 8 стоит в младшем разряде «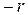 »=«–4».
»=«–4».
Пример 2.2. Число 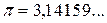 записать в виде позиционного разложения.
записать в виде позиционного разложения.
Решение: Имеем
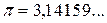 =
= 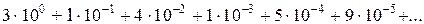 ;
;
старший разряд «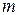 »=«0», младшего разряда нет (дробь бесконечная).
»=«0», младшего разряда нет (дробь бесконечная).
Определение 2.1. Первая слева, отличная от нуля цифра числа 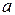 , и все расположенные справа от нее цифры (в том числе и нули), называются значащими.
, и все расположенные справа от нее цифры (в том числе и нули), называются значащими.
Если в числе есть нули, стоящие до первой ненулевой цифры, то они не являются значащими.
Пример 2.3. В ниже следующих числах подчеркнуты значащие цифры:
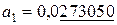 ,
, 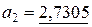 ,
, 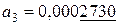 .
.
Определение 2.2. Значащая цифра 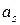 числа
числа 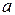 – верная, если предельная абсолютная погрешность
– верная, если предельная абсолютная погрешность 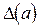 этого числа не превосходит половины единицы «
этого числа не превосходит половины единицы «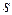 »-го разряда (разряда номера «
»-го разряда (разряда номера «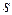 »), то есть
»), то есть
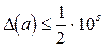 . (2.3)
. (2.3)
Пример 2.4. Найти верные цифры в приближенном числе для точного числа 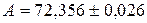 .
.
Решение: Имеем по условию 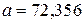 ,
, 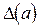 =0,026. Так как
=0,026. Так как
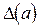 =0,026
=0,026 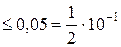 ,
,
то из неравенства (2.3) следует, что «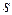 »=«–1». А это означает, что верной цифрой будет являться цифра, имеющая разряд «–1» (разряд десятых), то есть цифра 3. Верными также будут цифры 7 и 2 (стоящие левее тройки), так как для них выполняется неравенство (2.3):
»=«–1». А это означает, что верной цифрой будет являться цифра, имеющая разряд «–1» (разряд десятых), то есть цифра 3. Верными также будут цифры 7 и 2 (стоящие левее тройки), так как для них выполняется неравенство (2.3):
для цифры 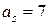 , «s»=«1» (разряд десятков):
, «s»=«1» (разряд десятков):
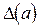 =0,026
=0,026 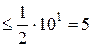 (верно),
(верно),
для цифры 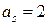 , «s»=«0» (разряд единиц):
, «s»=«0» (разряд единиц): 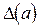 =0,026
=0,026 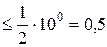 (верно).
(верно).
Цифры 5, 6 не будут являться верными. Например, для цифры 5 имеем
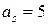 , «s»=«–2» (разряд сотых):
, «s»=«–2» (разряд сотых): 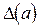 =0,026
=0,026 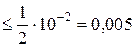 (неверно).
(неверно).
Итак, все значащие цифры, стоящие левее верной цифры, также являются верными. Цифра, стоящая правее какой-то верной цифры, не всегда является верной.
В теории погрешности нельзя, вообще говоря, откидывать значащие нули и тем более нельзя откидывать верные нули.
Принято считать следующее: если указано, что все значащие цифры числа 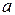 верные, то предельная абсолютная погрешность
верные, то предельная абсолютная погрешность 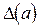 равна половине единицы младшего разряда «
равна половине единицы младшего разряда «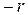 » в его позиционной форме записи:
» в его позиционной форме записи:
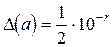 . (2.4)
. (2.4)
Пример 2.5. Известно, что в числах 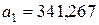 ,
, 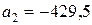 все цифры верные. Найти для них предельные абсолютные, относительные погрешности.
все цифры верные. Найти для них предельные абсолютные, относительные погрешности.
Решение:
1) Так как в числе 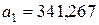 все цифры верные, то согласно (2.4)
все цифры верные, то согласно (2.4) 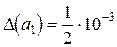 (последняя цифра 7 имеет младший разряд «
(последняя цифра 7 имеет младший разряд «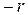 »=«–3»). Соответственно
»=«–3»). Соответственно 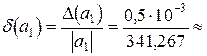
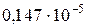 .
.
2) Для числа 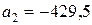 младший разряд «
младший разряд «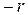 »=«–1», то есть
»=«–1», то есть 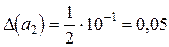 . Тогда
. Тогда 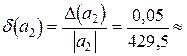 0,00012 = 0,012%.
0,00012 = 0,012%.
Если число 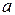 записано без погрешностей, то полагают, что все его значащие цифры верные (тогда практически задача нахождения
записано без погрешностей, то полагают, что все его значащие цифры верные (тогда практически задача нахождения 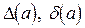 не вызывает труда).
не вызывает труда).
При многих вычислениях получаются результаты с большим числом значащих цифр. Тогда в зависимости от задачи целесообразно некоторые из них отбросить – округлить число. На практике обычно пользуются правилами округления чисел:
О.1) если первая отбрасываемая цифра меньше пяти, то последняя сохраняемая цифра не изменяется;
О.2) если первая отбрасываемая цифра больше или равна пяти и после нее есть ненулевые цифры, то последняя сохраняемая цифра увеличивается на единицу;
О.3) если первая отбрасываемая цифра равна пяти и после нее нет ненулевых цифр, то последняя сохраняемая цифра не изменяется, если она – четная, и увеличивается на единицу, если она – нечетная (правило четной цифры).
Покажем применимость сначала правила О.3. Пусть 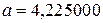 . Округление до сотых (то есть с сохранением первых двух цифр после запятой) дает результат
. Округление до сотых (то есть с сохранением первых двух цифр после запятой) дает результат 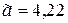 (первая отбрасываемая цифра 5, после нее стоят три нуля, первая сохраняемая цифра 2 не меняется, так как она четная). Если
(первая отбрасываемая цифра 5, после нее стоят три нуля, первая сохраняемая цифра 2 не меняется, так как она четная). Если 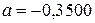 , то округление до десятых дает
, то округление до десятых дает 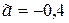 .
.
Пример 2.6. Округлить число 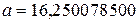 до каждого разряда.
до каждого разряда.
Решение: Округление числа удобнее оформить следующим образом:
| Результат округления | Правило | Комментарии к правилу |
до десятков 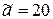 | О.2 | первая отбрасываемая цифра 6 (больше 5) |
до единиц 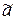 = 16 = 16 | О.1 | первая отбрасываемая цифра 2 (меньше 5) |
до десятых 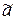 = 16,3 = 16,3 | О.2 | первая отбрасываемая цифра 5, после нее есть ненулевые цифры |
до сотых 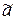 = 16,25 = 16,25 | О.1 | первая отбрасываемая цифра 0 (меньше 5) |
до тысячных 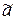 = 16,250 = 16,250 | О.1 | первая отбрасываемая цифра 0 (меньше 5) |
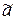 = 16,2501 = 16,2501 | О.2 | первая отбрасываемая цифра 7 (больше 5) |
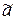 = 16,25008 = 16,25008 | О.2 | первая отбрасываемая цифра 8 (больше 5) |
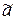 = 16,250078 = 16,250078 | О.3 | первая отбрасываемая цифра 5, после нее стоят только нули, первая сохраняемая цифра 8 не меняется, так как она четная |
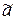 = 16,2500785 = 16,2500785 | О.1 | первая отбрасываемая цифра 0 (меньше 5) |
При округлении приближенного числа 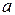 предельная абсолютная погрешность
предельная абсолютная погрешность 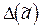 результата (округленного числа)
результата (округленного числа) 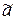 складывается из предельной абсолютной погрешности
складывается из предельной абсолютной погрешности 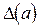 исходного числа
исходного числа 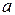 и погрешности округления
и погрешности округления 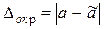 , то есть
, то есть
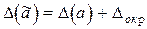
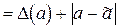 . (2.5)
. (2.5)
Пример 2.7. Округлить число 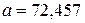 (
(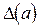 =0,0036) до числа
=0,0036) до числа 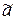 , оставив в нем только верные цифры. Найти
, оставив в нем только верные цифры. Найти 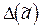 .
.
Решение:
1) Так как 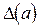 =0,0036
=0,0036 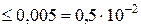 , то в числе
, то в числе 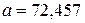 верными будут цифры 7, 2, 4, 5 (последняя цифра 7 не является верной):
верными будут цифры 7, 2, 4, 5 (последняя цифра 7 не является верной): 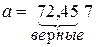 . Сначала округляем число
. Сначала округляем число 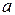 , сохраняя при этом верные цифры (то есть до сотых), откидывая последнюю цифру 7:
, сохраняя при этом верные цифры (то есть до сотых), откидывая последнюю цифру 7: 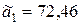 . Считаем погрешность округления и общую погрешность
. Считаем погрешность округления и общую погрешность 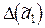 полученного числа
полученного числа 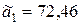 :
:
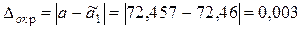 ,
,
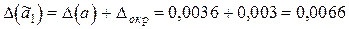 .
.
2) На этот раз 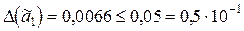 , то есть в числе
, то есть в числе 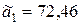 верными будут первые три цифры:
верными будут первые три цифры: 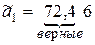 . Округляем число
. Округляем число 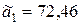 , сохраняя верные цифры (то есть до десятых):
, сохраняя верные цифры (то есть до десятых): 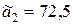 . Снова считаем погрешность округления и общую погрешность
. Снова считаем погрешность округления и общую погрешность 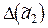
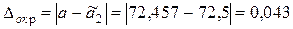 ,
,
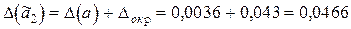 .
.
3) Так как 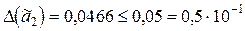 , то теперь в числе
, то теперь в числе 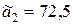 все цифры верные. Тогда
все цифры верные. Тогда 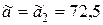 ,
, 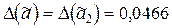 .
.
Ответ: 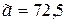 ,
, 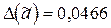 .
.
 2015-04-23
2015-04-23 15150
15150








