Форма Лагранжа

Пусть на отрезке [ a,b ] заданы n+ 1опорных (узловых) точек 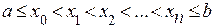. Пусть, кроме того, заданы n+ 1 действительных чисел y_j (j= 0,1,…… n) – значения функции. Тогда имеем следующую задачу интерполяции: найти многочлен 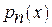степени не больше n такой, что 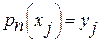для .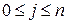

Данная интерполяция применяется тогда, когда известны только дискретные значения в узловых точках таблично заданной функции f (x), и для того, чтобы вычислить другие ее значения между (inter) точками или вне (extra) отрезка узловых точек. Найти многочлен 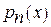- это значит найти все его n+ 1 коэффициентов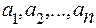

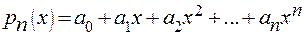(3)

Условия 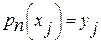определяют систему n уравнений:

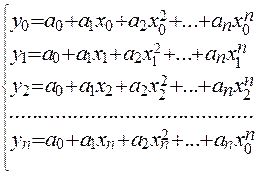(4)

Она имеет единственное решение, ввиду того, что определитель Ван-дер-Монда системы

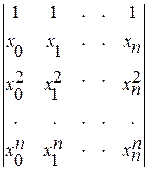
отличен от нуля. Решение этой системы уравнений представляет определенные сложности. Поэтому поступим следующим образом: будем строить многочлен n- ой степени в виде линейной комбинации 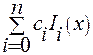многочленов той же степени. Приравнивая 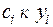, а базисные многочлены символу Кронекера имеем:

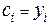
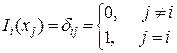для " i, j. (5)

получаем

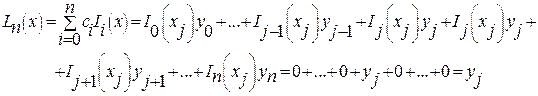
т.е. выполнено условие .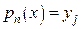

Теперь подберем многочлен 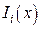удовлетворяющий условию (5). Равенство нулю любого 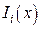во всех узлах, кроме i -го, можно обеспечить, записав его в виде

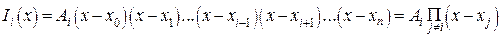(6)

Так как, в соответствии с (5), 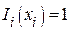, то из последнего выражения определяется нормировочный коэффициент :

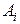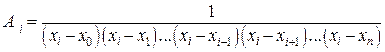(7)

Подставляя (7) в (6), получим для базисного многочлена в форме Лагранжа

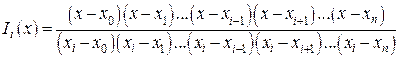(8)

и в результате искомый многочлен есть

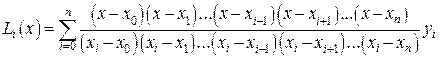(9)

Рассмотрим в качестве примеров первые три интерполяционные формулы.

Линейная интерполяция (n=1).

Для этого случая имеется информация о f (x) в двух точках (x ₀, y ₀) и (x ₁, y ₁). Очевидно, что искомый многочлен есть прямая проходящая через указанные точки, и определяется она с помощью двух базисных многочленов первой степен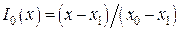и и 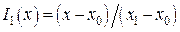. Тогда

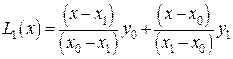(10)

Пример 1. Рассмотрим линейную интерполяцию функции 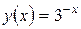на отрезке [0;6] по двум крайним точкам интервала y (0)=1, y (6)=1/729.

По формуле (10) получаем

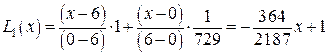(10^*)

Квадратичная интерполяция (n=2).

Теперь информация о функции f (x) имеется в трех точках, приведённых в таблице

i
x_i	x ₀	x ₁	x ₂
y_i	y ₀	y ₁	y ₂

По трем базисным многочленам:

, ,

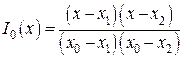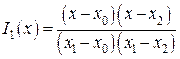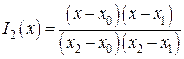
образуется квадратичная интерполяция

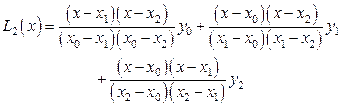(11)

Пример 2. Рассмотрим квадратичную интерполяцию той же функции 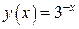на отрезке [0;6] по трем точкам: y (0)=1, y (3)=1/27, y (6)=1/729. По (11) получаем

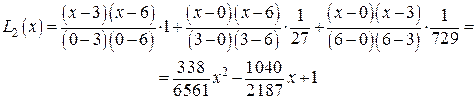(11^*)

Кубическая интерполяция (n=3).

Здесь образование интерполяционного многочлена осуществляется по четырем точкам

i
x_i	x ₀	x ₁	x ₂	x ₃
y_i	y ₀	y ₁	y ₂	y ₃

По формуле (9), записывая аналогично выражения для базисных многочленов, получаем

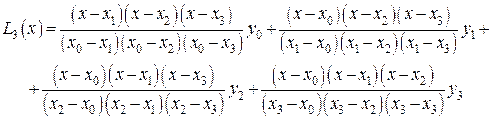(12)

Пример 3. Рассмотрим кубическую интерполяцию той же функции 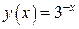на отрезке [0;6] по четырем точкам: y (0)=1, y (2)=1/9, y (4)=1/81, y (6)=1/729. По формуле (12) получаем

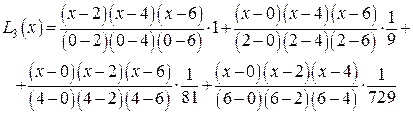
или после преобразований

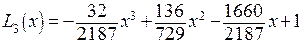(12^*)

Полученные приближения наглядно иллюстрируют графики зависимостей (10 - 12^*) построенные на рис. 1. Даже без соответствующих оценок видно, что кубическая интерполяция лучше описывает заданную функцию по сравнению с линейной и квадратичной.

Теперь оценим погрешность полученных приближений. По формуле (1) получаем:

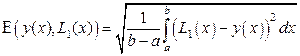, (13)

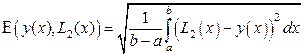, (14)

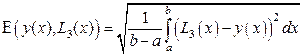, (15)

где а и b – границы отрезка [0,6].

Интегралы (13)-(15) вида 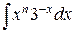вычисляем в элементарных функциях. Интегрируя (13)-(15), получаем:

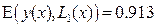
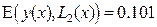
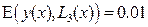
Из чего следует, что из трёх полученных аппроксимаций наиболее точно исходную функцию описывает кубическая аппроксимация .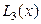

Для получения приближенных значений из отрезка [a;b] выберем внутри исследуемого интервала контрольную точку 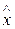и сравним значения функции с ее аппроксимациями. Пусть 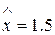. Подставляя 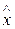в (10^*)-(12^*) и вычисляя по таблицам значение функции, получаем: 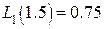, , 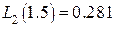, 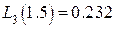а 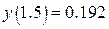. Ошибка вычисления по формуле 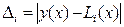составит: 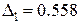, , 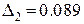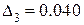. Откуда видно, что при наибольшем n ошибка минимальна, т.е. при кубической интерполяции.

Другой способ получить общую оценку (в произвольной точке) - из выражения для остаточного члена

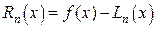
т.е. отклонения 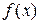от 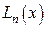. Считая, что 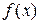на [a,b] непрерывно дифференцируема n+ 1 раз можно показать, что максимальная погрешность на этом интервале оценивается величиной

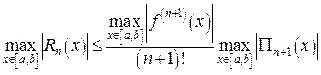(16)

где обозначено

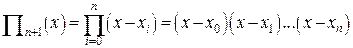
Из формулы (16) следует, что остаточный член с увеличением n уменьшается, следовательно, при этом выполняется условие 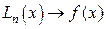, т.е. возрастает точность интерполяции.

Достоинством формулы Лагранжа, безусловно, является отсутствие каких-либо требований к расстояниям между узловыми точками, однако для практических вычислений она неудобна, так как при переходе к более высоким степеням многочлена приходится заново вычислять все входящие в него слагаемые. Поэтому чаще применяются полиномиальные интерполяции в более удобном разложении, при котором каждое следующее слагаемое просто добавляется к уже вычисленным.