Пер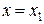вый интерполяционный многочлен Ньютона

При отличными от нуля будут первые два слагаемых и по условиям интерполяции

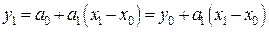
откуда

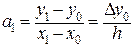. (22)

Следующая подстановка 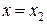с учетом полученных выражений приводит к уравнению относительно :

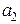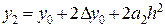
решение которого с учетом (20) примет вид

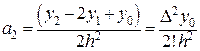(23)

Аналогично, при 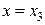получаем:

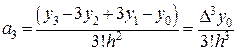(24)

Продолжая дальнейшие подстановки, можно убедиться, что для любого n справедливо:

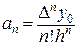(25)

Подставляя (22), (25) в (21), получаем полином:

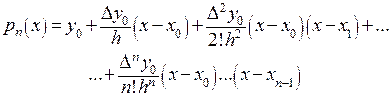(26)

который называют первым интерполяционным многочленом Ньютона..

Вводя новую переменную 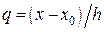и учитывая, что 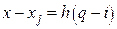, приходим к компактной записи первой формулы Ньютона.

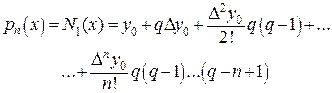(27)