Теорема сложения (Вентцель) вероятностей формулируется следующим образом.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
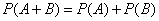
Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек:
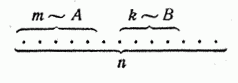
Предположим, что из этих случаев 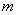 благоприятны событию
благоприятны событию 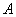 , а
, а 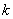 – событию
– событию 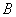 . Тогда
. Тогда
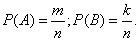
Так как события 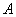 и
и 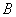 несовместимы, то нет таких случаев, которые благоприятны и
несовместимы, то нет таких случаев, которые благоприятны и 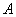 , и
, и 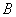 вместе. Следовательно, событию
вместе. Следовательно, событию 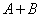 благоприятны
благоприятны 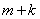 случаев и
случаев и
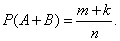
Подставляя полученные выражения в формулу получим тождество. Теорема доказана.
Обобщим теорему сложения на случай трех событий. Обозначая событие 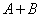 буквой
буквой 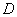 , и присоединяя к сумме еще одно событие
, и присоединяя к сумме еще одно событие 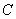 , легко доказать, что
, легко доказать, что
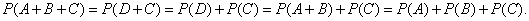
Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:
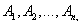
и докажем, что она будет справедлива для 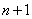 событий:
событий:
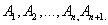
Обозначим:
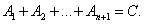
Имеем:
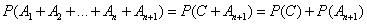 .
.
Но так как для n событий мы считаем теорему уже доказанной, то
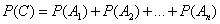 ,
,
откуда
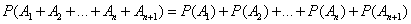 ,
,
что и требовалось доказать.
Таким образом, теорема сложения вероятностей применима к любому числу несовместных событий. Её удобнее записать в виде:
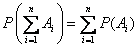
Отметим следствия, вытекающие из теоремы сложения вероятностей.
Следствие 1. Если события 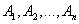 образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
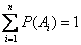 .
.
Доказательство. Так как события 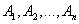 образуют полную группу, то появление хотя бы одного из них – достоверное событие:
образуют полную группу, то появление хотя бы одного из них – достоверное событие:
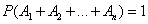 .
.
Так как 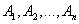 - несовместные события, то к ним применима теорема сложения вероятностей
- несовместные события, то к ним применима теорема сложения вероятностей
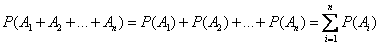 ,
,
откуда
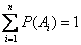 , что и требовалось доказать.
, что и требовалось доказать.
Противоположными событиями называются два несовместных события, образующих полную группу.
Событие, противоположное событию 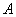 , принято обозначать
, принято обозначать 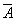 .
.
Примеры противоположных событий.
1) 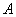 – попадание при выстреле,
– попадание при выстреле, 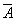 - промах при выстреле;
- промах при выстреле;
2) 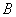 – выпадение герба при бросании монеты,
– выпадение герба при бросании монеты, 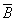 - выпадение цифры при бросании монеты;
- выпадение цифры при бросании монеты;
Следствие 2. Сумма вероятностей противоположных событий равна единице:
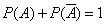 .
.
Это следствие есть частный случай следствия 1. Оно выделено особо ввиду его большой важности в практическом применении теории вероятностей. На практике весьма часто оказывается легче вычислить вероятность противоположного события 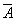 , чем вероятность прямого события
, чем вероятность прямого события 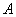 . В этих случаях вычисляют
. В этих случаях вычисляют 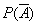 и находят
и находят 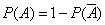 .
.
 2015-04-23
2015-04-23 715
715








