Параметры распределений

Параметром распределения называется величина, вычисляемая по множеству наблюдений и дающая определенную информацию о середине или других свойствах распределения: разбросе значений, асимметрии, эксцессе и др. Различные параметры можно свести в следующие группы.

Параметры центра распределения

1) Мода. Как уже говорилось, модой называется абсцисса вершины графика распределения. Мода обозначается символом M (Signet Roundhand ATT) или .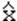

Если распределение не очень асимметрично, то мода - хорошее приближение центра совокупности, или середины выборки.

Если данные группированы и построена гистограмма, то группа с наибольшим значением частоты называется модальной группой (например, девятая группа в табл.2.5 и на рис.2.3). Середина модальной группы приблизительно соответствует значению моды.

2) Медиана. Медианой называется значение x, для которого 50% множества наблюдений или совокупности меньше этого значения, а 50% - больше его. Обозначение медианы Me или .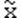

Медиана вычисляется следующим образом. Сначала упорядочивают наблюдения в порядке возрастания. Если число наблюдений нечетное, то медианой будет центральное значение. Если четное - то полусумма срединных значений.

Пример 2.5. Найти медиану выборки: S₁={9,3,5,8,4,11,13}.

После упорядочения: S_1у={3,4,5,8,9,11,13}. Медиана для нечетного числа наблюдений: 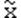= 8.

Пример 2.6. Дана выборка: S₂={20,9,13,1,4,11}. Найти медиану.

Упорядоченная выборка: S_2у={1,4,9,11,13,20}. Медиана для четного числа наблюдений:

9+11

Me = ¾¾¾ = 10.

3) Арифметическое среднее 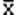. Арифметическое среднее множества из N наблюдений получается суммированием всех значений и делением этой суммы на N.

Для группированных данных сначала составляется частотная таблица, а затем 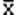вычисляется по формуле взвешенного среднего:

f₁x₁+f₂x₂+... +f_ix_i+... +f_Kx_K

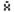= ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾, (2.13)

f₁+f₂+... +f_i+... +f_K

где x₁, x₂,¼x_i,¼x_K - среднее группы,

f₁, f₂,¼f_i,¼f_K - относительная частота группы,

K - количество групп.

Пример 2.7. Дана частотная таблица:

среднее группы xi
Частота группы mi

Для вычисления арифметического среднего применяем формулу:

_K

Sm_ix_i

_i=1

`X = ¾¾¾. (2.13а)

N

В формуле (2.13а) m_i - частота группы, выступающая здесь как «вес» наблюдения, N - объем выборки. По данным примера 2.7:

4·3 + 2·4 + 1·5 + 2·9

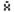= ¾¾¾¾¾¾¾¾¾¾¾¾¾ = 4,78.

4 + 2 + 1 + 2

Если данные группированы, то формула (2.13) дает всего лишь приближенное значение 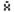. Использование этой формулы основано на предположении, что каждое наблюдение в группе совпадает со средним в этой группе, что, конечно, неверно. С другой стороны, получающиеся ошибки имеют тенденцию к взаимному погашению, т.к. в общем случае одни наблюдения группы имеют значения выше среднего, другие - ниже. Поэтому приближение, основанное на группировании (агрегатировании) данных, как правило, бывает хорошим.

4) Взаимосвязь между модой, медианой и средним. Если распределение симметрично, то:

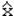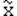= =`X, (2.14)

т.е все они совпадают. Для унимодального и не очень асимметричного распределения существует приближенная формула связи:

X - 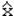» 3(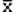 - 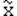). (2.15)

(см.рис.2.7).

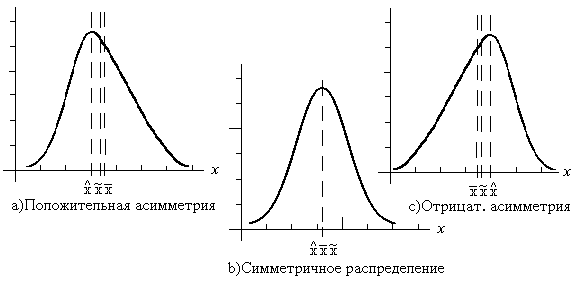
Рис.2.7. Взаимное расположение среднего арифметического, моды и медианы в

картинах симметричного и слабо асимметричных распределений.

Параметры разброса

1) Вариация 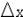. Вариация - простейшая мера разброса множества наблюдений. Она представляет собой разность крайних значений выборки:

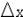= x_max- x_min (2.16)

Пример 2.8. Дана выборка: S={8,3,1,20,15,5,12}. Рассчитать вариацию. Воспользуемся формулой (2.16):

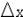= 20-1 = 19.

Вариацией пользуются при работе с малыми выборками. Например, при контроле качества, состоящем в проверке величины отклонений размеров массовой продукции от определенных границ.

2) Отклонение от средней d (центрированная случайная величина).

Этот параметр является более эффективной мерой разброса,т.к. опирается не на два крайних значения, как предыдущий, а на все наблюдения:

d = (x_i - 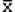), i=(1,2,....,N) (2.17)

Для выборки X={1,5,8,6}, имеющей 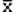=5, множество d:

d={- 4,0,+3,+1}.

Неудобство этого параметра состоит в том, что он определяется большим числом значений (равным величине выборки N).

3) Стандартное отклонение - это мера рассеивания, обозначаемая s и вычисляемая по формуле:

S(x_i- 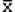)²

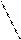_N

s = ¾¾¾¾¾¾ (2.18)

N

Параметр s называют также среднеквадратическим отклонением (с.к.о.).

Квадрат стандартного отклонения называется дисперсией (т.е. рассеянием):

D = s² (2.19)

Пример 2.9. Для выборки Y={4,8,6,3,7,2}:

n центрированная выборка (отклонение от средней):

d_i = {-1,3,1,-2,2,-3};

n дисперсия:

_N

S(d_i)²

_i=1

D = ¾¾¾¾ = 28/6 = 4,667;

N

n с.к.о.: __

s = Ö D = 2,16.

Следует обратить внимание, что, согласно формулам (2.18) и (2.19), C.К.О. имеет размерность измерителя, а дисперсия - квадрата измерителя.

3) Соотношение между 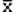, б и распределением. Значение 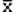приближенно указывает, где расположен центр распределения, а б несет информацию о его разбросе около 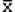. Для большинства унимодальных распределений выполняются следующие соотношения:

n 95% распределения лежит между значениями: (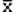 -2б) и ( 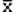+2б), т.е. в среднем менее 1 наблюдения из выборки объемом N=20 лежит за пределами этого интервала;

n более 99% распределения заключено между: (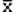 -3б) и ( 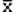+3б), иначе говоря, за пределами интервала 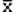±б лежит в среднем менее одного наблюдения из выборки объемом N=100). На этом свойстве распределений основано правило трех сигм: при статистической обработке наблюдений значения выборки, выходящие за пределы интервала «трех сигм», отбрасываются, как маловероятные, т.е. относящиеся к промахам измерений.

Эти свойства можно проиллюстрировать следующим примером. Если рост учащихся L распределен нормально (распределение имеет строго симметричную форму) и при этом`L=178 cм и s=8, то приближенные 95% и 99%-ные границы распределения будут: (178±16) и (178±24) см.

Параметр асимметрии

Из соотношения между средней и модой видно, что для распределения с положительной асимметрией 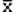> 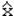,а с отрицательной 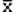> 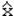.Чем больше асимметрия, тем больше разность между этими величинами, т.е. разность ( 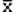- 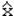) можно рассматривать как меру асимметрии. Для получения безразмерной величины в качестве такой меры рассчитывают 1-й коэффициент Пирсона:

( - )

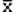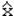A₁ = ¾¾¾¾. (2.20)

s

Второй коэффициент Пирсона приблизительно равен первому, если при расчете вместо моды взять медиану:

3( - )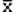

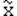A₂ = ¾¾¾¾¾. (2.21)

s

Оба коэффициента асимметрии равны нулю для симметричных распределений, положительны для положительных и отрицательны для отрицательных асимметрий (ср. формулы 2.20 и 2.21 с кривыми на рис.2.7).

Параметр островершинности

Островершинность или туповершинность картины распределения оценивается показателем Линдберга:

E _x = P - 38,29 (2.22)

где P - доля (в %) количества измерений, лежащих в интервале ±s/2 от среднего арифметического. Для плосковершинных распределений этот показатель отрицателен, для островершинных - положителен.