Глава 4.
Тема 1.
Дифференцирование. Основные определения и правила.
Определение 1. 1. Пусть функция 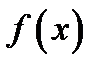 определена в открытом интервале
определена в открытом интервале 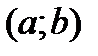 и пусть точка
и пусть точка 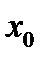 принадлежит
принадлежит 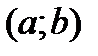 . Производной функции
. Производной функции 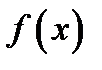 в точке
в точке 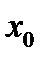 назовем величину
назовем величину
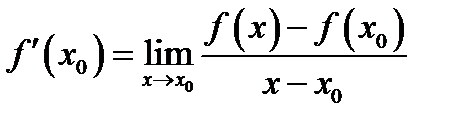 (1.1)
(1.1)
если предельное значение (1.1) существует и конечно. Функцию, имеющую производную будем называть дифференцируемой функцией.
Секущие и касательные прямые к графику функции 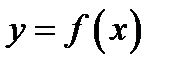 .
.
Определение 1. 2.
| M1 |
| M0 |
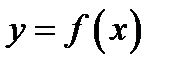 назовём прямую, проходящую через две точки лежащие на графике:
назовём прямую, проходящую через две точки лежащие на графике: 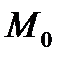
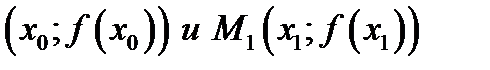 . Вычислим угловой коэффициент секущей прямой
. Вычислим угловой коэффициент секущей прямой 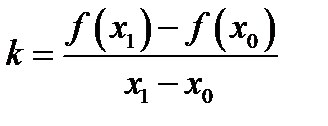
Тогда уравнение этой прямой принимает вид: 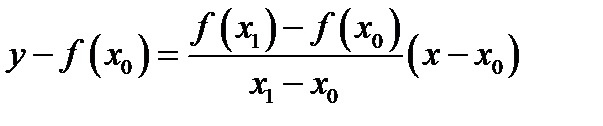 рис.1а.
рис.1а.

рис.1а.
Если теперь точку 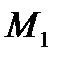 неограниченно приближать вдоль графика к точке
неограниченно приближать вдоль графика к точке 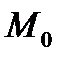 , то наклон секущей будет меняться. Допустим, что существует предельное значение
, то наклон секущей будет меняться. Допустим, что существует предельное значение 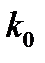 углового коэффициента
углового коэффициента 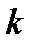 (при условии
(при условии 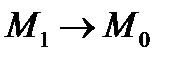 ), то есть
), то есть
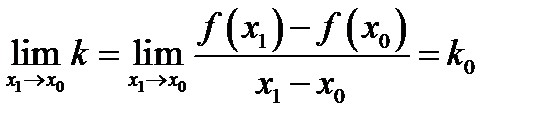 (1.2)
(1.2)
Определение 1.3. Прямая 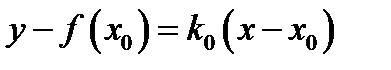 называется касательной прямой к графику функции с точкой касания
называется касательной прямой к графику функции с точкой касания 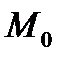 . Сравнивая формулы (1.1) и (1.2) получаем
. Сравнивая формулы (1.1) и (1.2) получаем 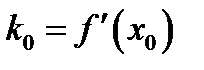 и уравнение касательной прямой запишется в виде
и уравнение касательной прямой запишется в виде
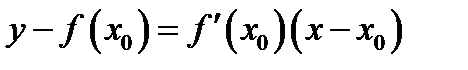 (1.3)
(1.3)
Если 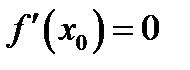 , то касательная, проходящая через точку касания
, то касательная, проходящая через точку касания 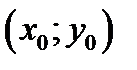 , параллельна оси ОХ и её уравнение будет таким
, параллельна оси ОХ и её уравнение будет таким 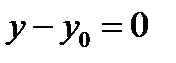 .
.
 2015-04-23
2015-04-23 452
452







