Пусть 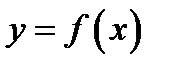 непрерывна в точке
непрерывна в точке 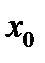 . Если при вычислении углового коэффициента касательной
. Если при вычислении углового коэффициента касательной
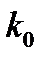 окажется
окажется
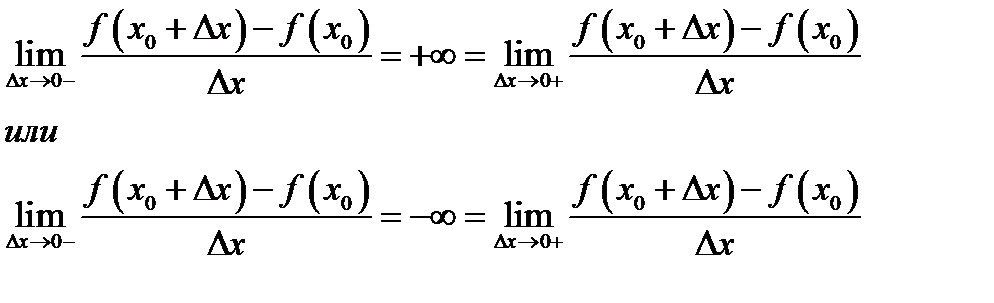 (1.4)
(1.4)
То будем говорить, что в точке 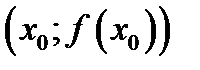 график функции имеет вертикальную касательную,
график функции имеет вертикальную касательную,
задаваемую уравнением (рис.1б)
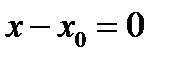 (1.5)
(1.5)
рис.1.б.
Пример 1. 1. Пусть на графике функции 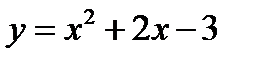 заданы две точки
заданы две точки 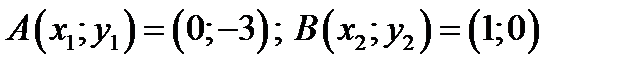 . Найдем уравнения:
. Найдем уравнения:
1) Секущей прямой проходящей через точки 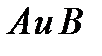
2) Уравнения касательных прямых к графику проведённых
в точках 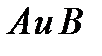 .
.
Решение. 1) Определяем угловой коэффициент секущей прямой, проходящей через точки 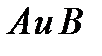
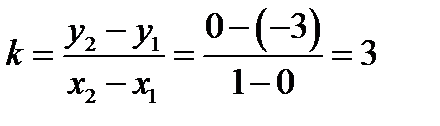 . Выписываем уравнение секущей
. Выписываем уравнение секущей 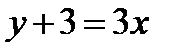 или
или 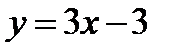 . Чтобы написать уравнение касательной нужно найти её угловой коэффициент. Согласно определению 1.3 угловой коэффициент касательной равен значению производной данной функции в точке касания:
. Чтобы написать уравнение касательной нужно найти её угловой коэффициент. Согласно определению 1.3 угловой коэффициент касательной равен значению производной данной функции в точке касания: 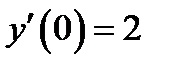 и
и 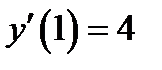 . Подставляя данные в формулу (1.3), выписываем уравнения касательных
. Подставляя данные в формулу (1.3), выписываем уравнения касательных
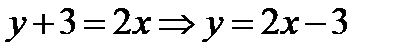 ;
; 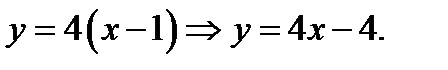
С помощью касательных определяют углы между графиками функций в точке их пересечения.
Определение 1.4. Углом между графиками функций
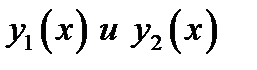 в точке их пересечения называется угол между их касательными прямыми в этой точке рис. 2. Этот угол находим по формуле
в точке их пересечения называется угол между их касательными прямыми в этой точке рис. 2. Этот угол находим по формуле
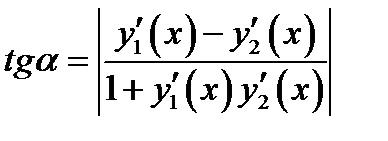 (1.4)
(1.4)
По формуле (1.4) определяется острый угол между
рис.2. касательными прямыми.
Замечание. Определение производной удобнее записывать и использовать с помощью приращений.
Определение 1.5. Приращением аргумента называют разность 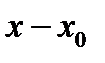 и обозначают через
и обозначают через 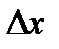
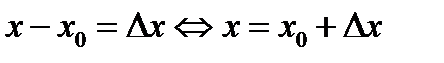 . Разность
. Разность 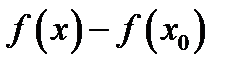 =
= 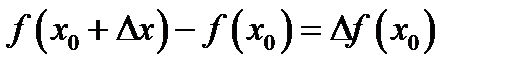 называют приращением функции.
называют приращением функции.
Таким образом, определение производной можно переписать так
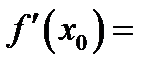
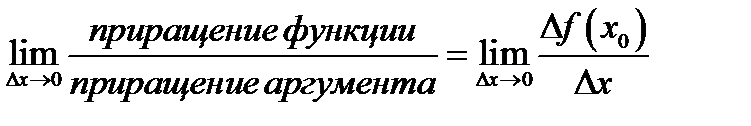 (1.5)
(1.5)
Замечание. Производные можно записывать следующими символами 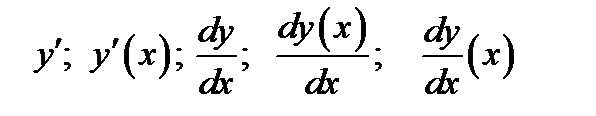
Пример 1.2. Пользуясь определением (1.5), найдите производные функций 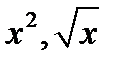 в точке
в точке 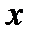 .
.
Решение. Используя определение производной (4.5), вычисляем приращение функции в точке 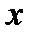
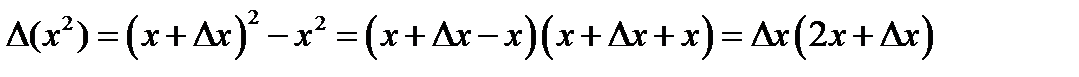 . Тогда
. Тогда 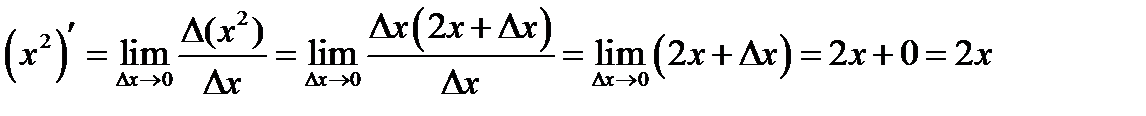 .
.
Пользуясь определением (1.5), найдём производную функции 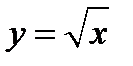 .
.
По определению имеем 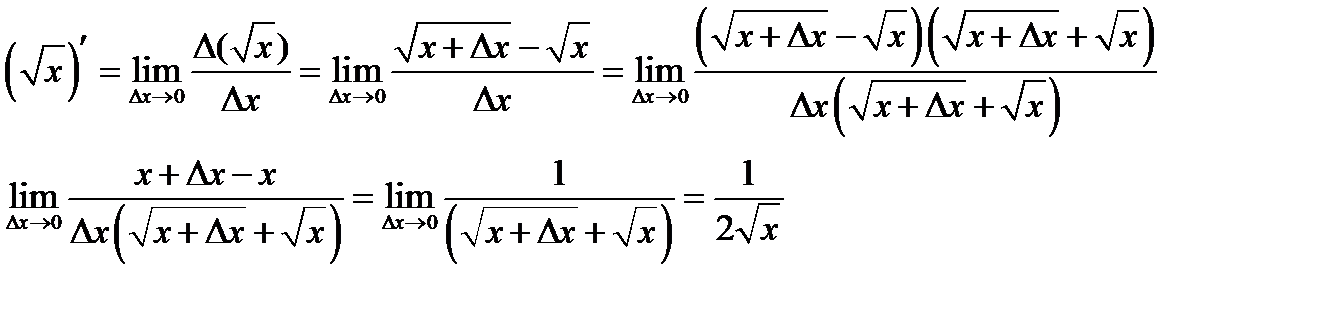
Физический смысл производной. Пусть путь, пройденный точкой, движущейся вдоль прямой, меняется со временем по закону 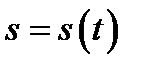 , тогда средняя скорость за период времени
, тогда средняя скорость за период времени 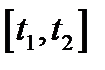 определяется как
определяется как 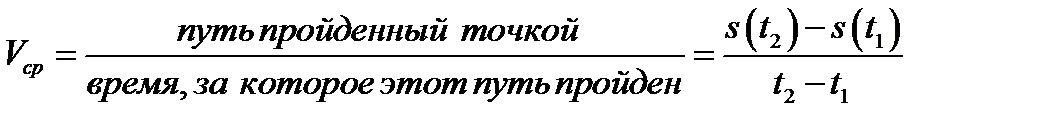 ;
;
Мгновенная скорость в момент времени 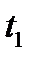 есть (по определению) предельное значение средней скорости
есть (по определению) предельное значение средней скорости 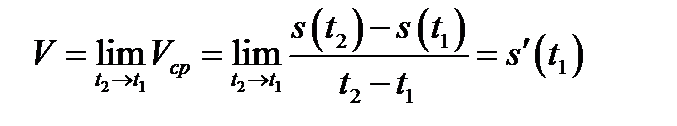 ;
;
 2015-04-23
2015-04-23 5081
5081
