Метод Эйлера

Рассмотрим этот метод на пример системы (11.3) (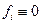). Решение этой системы в виде фундаментальной системы решений: 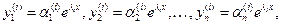(11.5)

где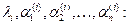

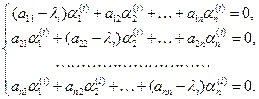
Эта система имеет ненулевое решение, когда ее определитель равен нулю, т.е. уравнение вида 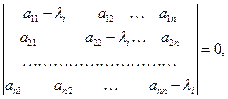(11.6)

называемое характеристическим.

Раскрывая определитель, получаем алгебраическое уравнение n -го порядка относительно 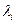с действительными постоянными коэффициентами, которое имеет n корней (с учетом их кратности).

Возможны следующие случаи, когда корни характеристического уравнения (11.6) являются:

1) действительными и различными

2) комплексными и различными

3) действительными, среди которых есть кратные

4) комплексные, среди которых есть кратные.

Пример 11.2. Решить методом Эйлера систему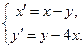

Приведем исходную систему к следующему виду:

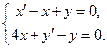(11.7)

Решение этой системы будем искать в виде

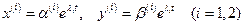. Подставим его в (11.7)

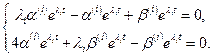
Сокращаем на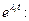

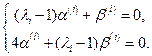(11.8)

Составляем характеристическое уравнение:

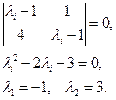
Замечание. Решения характеристического уравнения (11.6) являются собственными значениями, для каждого из которых строится собственный вектор.

Для 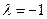система (11.8) имеет вид

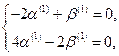
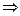
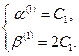Тогда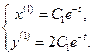

Для 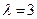система (11.8) имеет вид

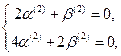
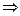
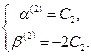. Тогда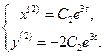

Общее решение исходной системы имеет вид

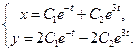
Задания для работы на семинаре:

Учебные материалы по курсу "Дифференциальные и разностные уравнения".

Составители:Андреев В.Б., Кюркчан А.Г., Чернявский В.М. ~ М.: ВШЭ, 1996.

1) Стр. 124, № 786-812,

2) Стр. 125, № 826-845.