Пусть f(x) неопределенна на [a,b]. Возмем на нем произвольную т. x и рассмотрим определенный интеграл:
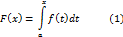
он сужествует для всех x 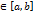 и является ф-ей своего верхнего предела.
и является ф-ей своего верхнего предела.
Теорема:
Пусть f(x) – непрерывна на [a,b], тогда ф-я (1) имеет производную в любой т. x 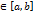 , причем F’(x) = f(x).
, причем F’(x) = f(x).
Другими словами:
Производная от определенного интеграла по его верхнему пределу, равна значению подинтегральной ф-и в верхнем пределе.
Док-во:
Дадим аргументу x прирожение 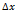 , что (x +
, что (x + 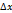 )
) 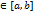 , тогда ф-я F получить прирощение
, тогда ф-я F получить прирощение 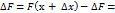
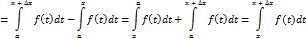
Применяем т. о Среднем значинии ф-ии:
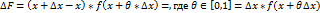
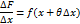
Переходим к lim при 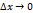
F’(x) = 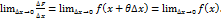
 2015-04-20
2015-04-20 1060
1060








