Пусть ф-я f(x)-непрерывна на [a,b], а ф-я F(x) первообразная. Тогда:
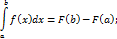
Док-во:
Рассмотрим ф-ю Ф(х) = 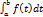 . Эта ф-я является первообразной для f(x) на [a,b].
. Эта ф-я является первообразной для f(x) на [a,b].
А любые две первообразные отличаются друг от друга на произвольную постоянную.
Ф(х) = F(x) + C, т.е. 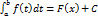
Замена переменной в определенном интеграле.
Пусть f (x) – непрерывная на отрезке [ a; b ] функция, а функция 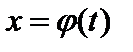 и ее производная
и ее производная 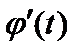 непрерывны на отрезке
непрерывны на отрезке 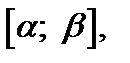 где
где 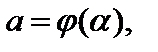
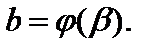 Тогда справедлива формула
Тогда справедлива формула
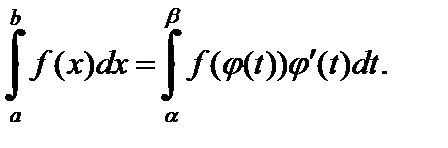
Интегрирование четных и нечетных функций.

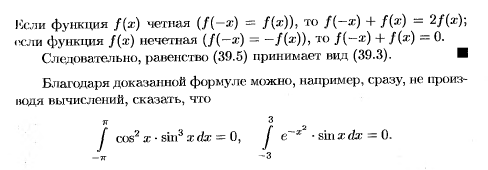
 2015-04-20
2015-04-20 858
858








