Пусть ф-я f(x) определена на отрезке [a,b]. Разобьем его на n-частей и составим интегральные суммы.
Число I называется пределом интегральных сумм:
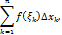
ф-ии f(x) на отрезке [a,b], если для любого ε > 0 существует δ>0, что для любого разбиения отрезка [a,b] на части с длинами 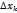 < δ, неравенство:
< δ, неравенство:
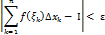
выполняются при любом выборе точек 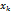 .
.
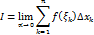
Если при любом разбиении отрезка [a,b] на части и при любом выборе точек 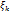 на их интегральные суммы имеют один и тот же конечный предел, то этот предел называется определенным интегралом и обозначается:
на их интегральные суммы имеют один и тот же конечный предел, то этот предел называется определенным интегралом и обозначается:
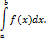
Геометрический смысл определенного интеграла: определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.
Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V (t), 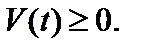 Тогда путь, пройденный точкой за промежуток времени от
Тогда путь, пройденный точкой за промежуток времени от 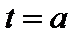 до
до 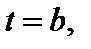 равен определенному интегралу от скорости:
равен определенному интегралу от скорости:
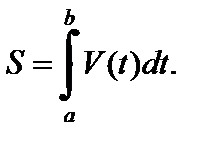
 2015-04-20
2015-04-20 15216
15216
