Несобственные интегралы второго рода. Теоремы сравнения

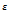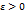Пусть ф-я f(x) интегрируема на [a, b- ] при сколь угодно малом , но неограниченав интервале (b- 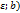. Определим, что мы будем понимать под символом:

Рассмотрим ф-ю I() =

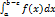
Если при 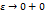ф-я I() имеет конечный предел, то несобственный интеграл сходится и по определению он равен:

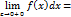
Аналогично если ф-я f(x) неограниченна только в интервале 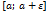несобственный интеграл 2-го рода определяется так:

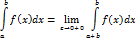
Теоремы сравнения:

1. Пусть f(x) и 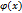интегрируемы на [a,b- ] и для них выполняется условие 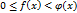, x 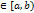. Тогда:

1) Если сходится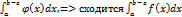

2) Если расходится =>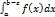

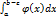
2. Пусть положительные на [a,b] ф-и f(x) и 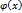– неограниченны только в окрестности т. b, 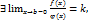тогда:

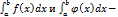сходятся или расходятся одновременно.