Необходимым условием существования интеграла является ограниченность функции f(x). Поэтому интеграл от неограниченной функции в обычном смысле не существует. Однако, можно распространить определение определенного интеграла на неограниченные функции при помощи введения некоторых понятий.
Случай неограниченной области:
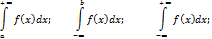
Пусть функция f(x) определена для всех x >= a и интегрируема на каждом конечном отрезке от a до b. Рассмотрим ф-ю аргумента b.
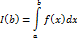
Если при b→+ 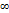 ф-я I(b) имеет конечный предел, то мы называем несобственный интеграл – сходящимся.
ф-я I(b) имеет конечный предел, то мы называем несобственный интеграл – сходящимся.
Если при b→+ 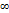 ф-я I(b) не имеет конечный предел, то мы называем несобственный интеграл – несходящимся.
ф-я I(b) не имеет конечный предел, то мы называем несобственный интеграл – несходящимся.
Теоремы сравнения:
Ø Пусть на [a,b] при сущ. b > a, ф-и f(x) и φ(x) интегрир. И f(x) <= φ(x)
Тогда:1) 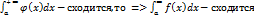
2) 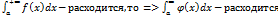
Ø Пусть ф-и f(x) и 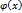 непрерывны и неотриц. для всех x>=a, пусть
непрерывны и неотриц. для всех x>=a, пусть 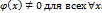 Тогда если существует конечный предел
Тогда если существует конечный предел 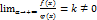 , то)
, то) 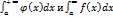 сходится и расходится одновременно.
сходится и расходится одновременно.
Ø Если существует такое число 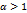 , что для всех достаточно больших x:
, что для всех достаточно больших x: 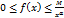 , где М>0 и не зависит от х, то
, где М>0 и не зависит от х, то 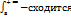
Если для Больших х: 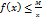 , от
, от 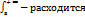 .
.
 2015-04-20
2015-04-20 2166
2166








