Частные производные. Геометрический смысл частных производных функции двух переменных

Частной производной по переменной х функции 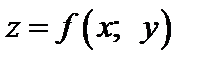в точке 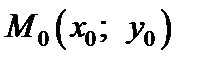называется предел

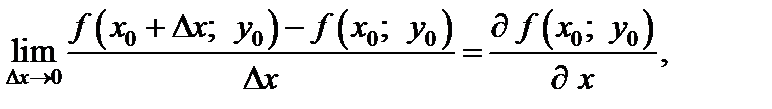(18.1)

если он существует.

Производную (18.1) обозначают также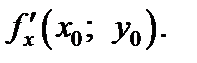

Частной производной по переменной у функции 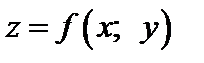в точке 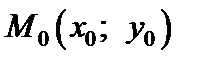называется предел

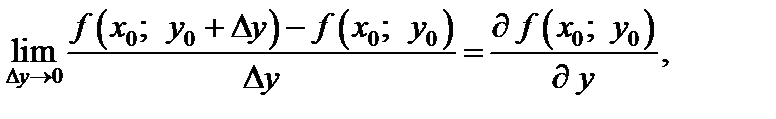(18.2)

если он существует.

Производную (18.2) обозначают также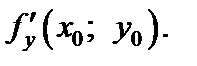

Если частные производные определены на множестве 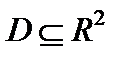и 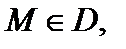то они являются функциями двух переменных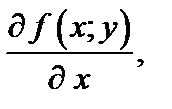

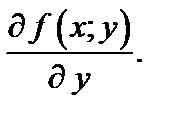
Для функции трех переменных 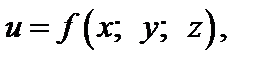в случае их существования, аналогично определяют три частные производные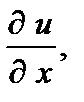

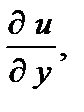
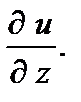
Геометрически, частная производная является производной по направлению одной из координатных осей. Частная производная функции f в точке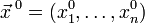

по координате xk равна производной 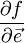по направлению где единица стоит на k-ом месте.