Криволинейные интегралы второго рода. Вычисления

Пусть на плоскости xOy задана гладкая незамкнутая кривая L, и на этой кривой определена вектор-функция

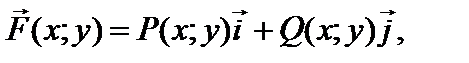
где P (x; y) и Q (x; y) – непрерывные функции.

Разобьем указанную кривую L произвольным образом на элементарные дуги 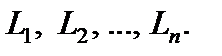На каждой из элементарных дуг 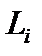выберем произвольную точку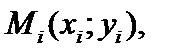

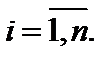
Составим произведение значения функции 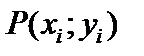на длину проекци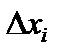и дуги 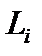на ось Ox и произведение значения функции 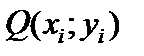на длину проекци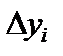и дуги 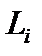на ось Oy. Запишем предельную сумму:

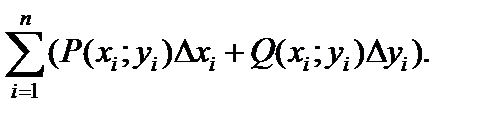
Обозначим через 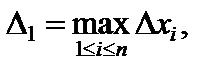а через 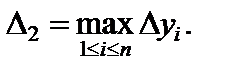Устремим 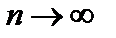так, чтобы 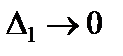и 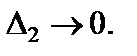Если существует предел интегральных сумм, который не зависит ни от способа разбиения кривой L на части, ни от выбора точек 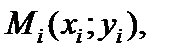то этот предел называется криволинейным интегралом 2-го рода от функции 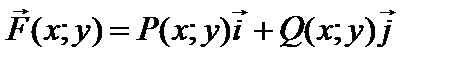по координатам x и y:

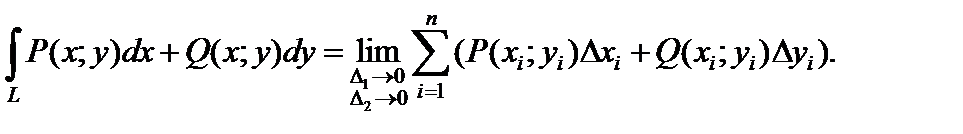
Если L – гладкая кривая в трехмерном пространстве, а 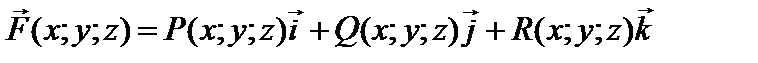– вектор-функция, заданная на L, причем P (x; y; z), Q (x; y; z) и R (x; y; z) – непрерывные функции в точках этой кривой, то в случае существования предела и при аналогичных плоской кривой условиях криволинейный интеграл 2-го рода по координатам x, y и z определяется равенством:

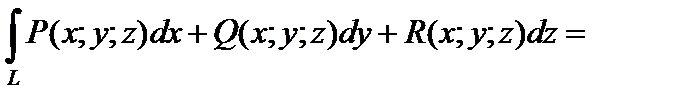
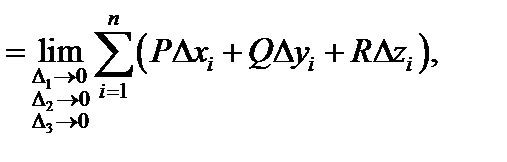
где в правой части формулы 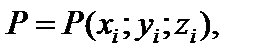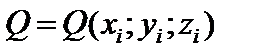и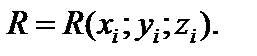

Если кривая L представляет собой замкнутый контур (т. е. начало кривой и ее конец совпадают), вводят понятие положительного и отрицательного направлений обхода контура. Положительным направлением обхода контура называется такое направление, при которомлиния интегрирования обходится против хода часовой стрелки. Противоположное ему направление обхода контура называется отрицательным. При этом считают, что 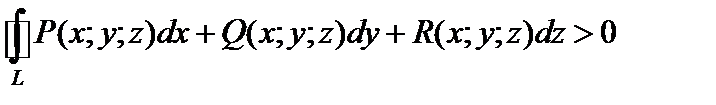при положительном направлении обхода контура L.