2015-04-20
655
| Если область интегрирования при вычислении тройного интеграла представляет собой тело, ограниченное сферой или некоторой ее частью, целесообразно перейти к сферическим координатам. |
Формулы перехода от декартовых координат x, y и z к сферическим координатам r,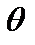 
и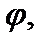 
исходя из приведенного чертежа, имеют вид:
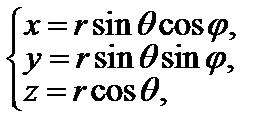(25.5)
где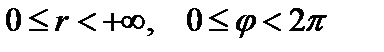 
(или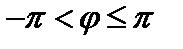 
), 
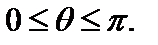
Формула замены переменных в тройном интеграле при переходе к сферическим координатам имеет вид:
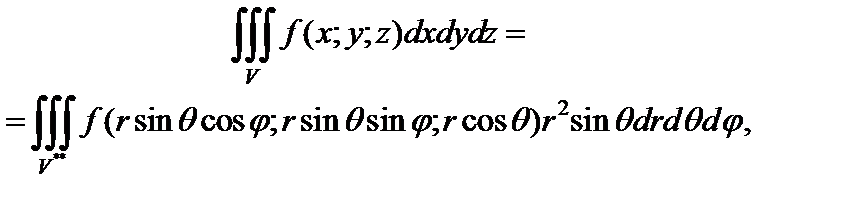(25.6)
где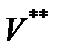 
– область в сферической системе координат, соответствующая области V в декартовой системе координат;
f (x; y; z) – функция, непрерывная в этой области.
