Пусть на плоскости xOy задана гладкая незамкнутая кривая L с началом в точке A и концом в точке B, не имеющая самопересечений. Допустим, что на этой кривой определена непрерывная функция 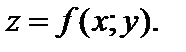 Разобьем указанную кривую L произвольным образом на элементарные дуги
Разобьем указанную кривую L произвольным образом на элементарные дуги 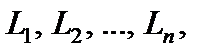 длины которых будем считать соответственно равными
длины которых будем считать соответственно равными 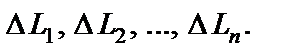 На каждой из элементарных дуг
На каждой из элементарных дуг 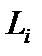 выберем произвольную точку
выберем произвольную точку 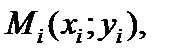
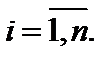 Обозначим через
Обозначим через 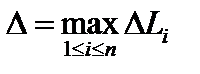 и составим интегральную сумму
и составим интегральную сумму
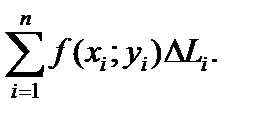 Устремим
Устремим так, чтобы
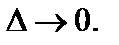 Если существует предел интегральных сумм, который не зависит ни от способа разбиения кривой L на части, ни от выбора точек
Если существует предел интегральных сумм, который не зависит ни от способа разбиения кривой L на части, ни от выбора точек 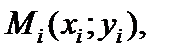 то этот предел называется криволинейным интегралом 1-го рода от функции f (x; y) вдоль кривой L:
то этот предел называется криволинейным интегралом 1-го рода от функции f (x; y) вдоль кривой L:
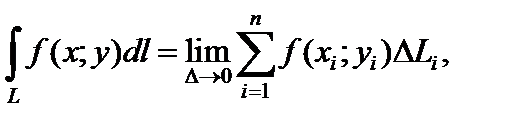 dl называют дифференциалом длины дуги, а саму кривую L – линией интегрирования. При этом говорят, что функция f (x; y) интегрируема по кривой L.
dl называют дифференциалом длины дуги, а саму кривую L – линией интегрирования. При этом говорят, что функция f (x; y) интегрируема по кривой L.
Если L – гладкая кривая в трехмерном пространстве без самопересечений, а f (x; y; z) – непрерывная функция в точках этой кривой, то криволинейный интеграл 1-го рода по этой кривой определяется равенством
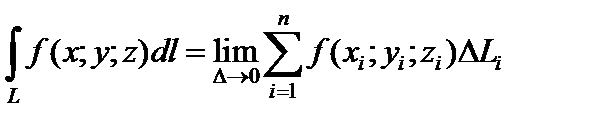 в случае существования предела и при аналогичных плоской кривой условиях.
в случае существования предела и при аналогичных плоской кривой условиях.
Если кривая L представляет собой замкнутый контур (т. е. начало кривой и ее конец совпадают), используют специальное обозначение: 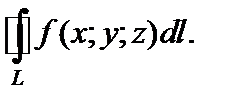 Достаточное условие интегрируемости функции: если функция определена и непрерывна в точках гладкой, не имеющей самопересечений, кривой, то она интегрируема по этой кривой.
Достаточное условие интегрируемости функции: если функция определена и непрерывна в точках гладкой, не имеющей самопересечений, кривой, то она интегрируема по этой кривой.
Если функции f (x; y), f 1(x; y) и f 2(x; y) интегрируемы по гладкой кривой L, то справедливы следующие свойства:
1) линейность:
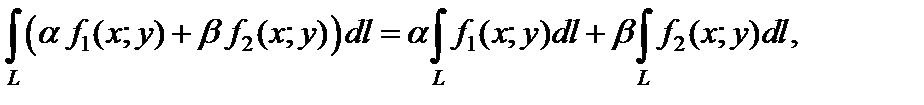 где
где 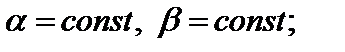
2) аддитивность: если гладкая или кусочно-гладкая кривая L состоит из конечного числа гладких дуг 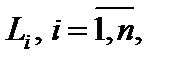 то
то
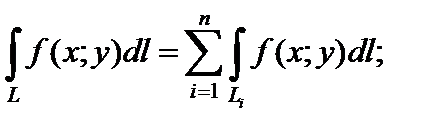 3) независимость от направления пути интегрирования: если кривая L соединяет точки A и B, то
3) независимость от направления пути интегрирования: если кривая L соединяет точки A и B, то 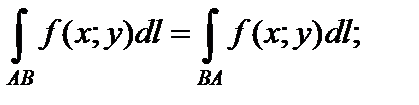
4) оценка модуля интеграла:
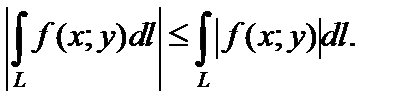
 2015-04-20
2015-04-20 1323
1323








