Дуговая и точечная эластичность

Рассмотрим два метода определения ценовой эластичности спроса.

1. Дуговой метод. Обратимся к кривой спроса на рис. 2.11.

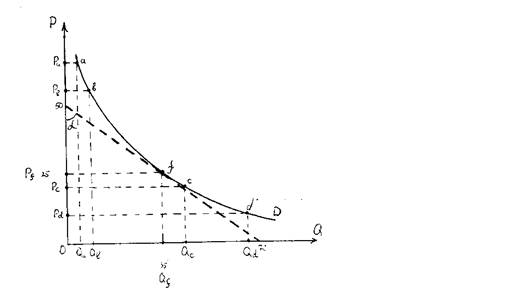
Рис. 2.11. Определение ценовой эластичности спроса.

Ценовая эластичность спроса будет различной на различных ее участках. Так, на участке ab спрос будет неэластичным, а на участке cd – эластичным. Измеренная на этих участках эластичность называется дуговой эластичностью.

Дуговая эластичность – это эластичность, измеренная между двумя точками кривой.

Фактически приведенная нами выше формула 2.8 была формулой дуговой эластичности. В числителе в ней фигурировало изменение количества блага в процентном выражении. Если мы отвлечемся от процентного выражения этого изменения и посмотрим, что есть относительное изменение Q, то нетрудно определить его как Q / Q. Аналогичным образом относительное изменение цены можно представить как Р / Р. Тогда ценовая эластичность спроса может быть представлена:

_D = 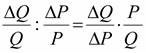(2.9)

В качестве Q берется разность между двумя значениями спроса на благо. Например, применительно к рис. 2.11 это могут быть разности (Q _a Q _b) или (Q _c Q _d). В качестве Р берется разность между двумя значениями цены, допустим (P _a P _b) или (P _c P _d). Проблема заключается в том, какое из двух значений количества блага и цены использовать в формуле 2.9 в качестве значений Q и Р. Понятно, что при разных значениях получается разный результат. Решение проблемы заключается в том, чтобы использовать среднее арифметическое двух значений. В таком случае мы измеряем некую среднюю эластичность на спрямляющих дуги отрезках ab и cd, и формула дуговой эластичности принимает вид:

_D = ,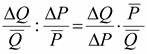

где 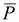= (P _a + P _b)/2 или 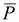= (P _с + P _d)/2, а 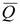= (Q _a + Q _b)/2 или 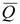= (Q _с + Q _d)/2 (опять же нижние индексы отвечают обозначениям из рис. 2.11). Если же мы рассмотрим некий общий случай и обозначим значения количеств блага и цены как Q ₁, Q ₂ и P ₁, P ₂, соответственно, то окончательно формулу дуговой эластичности после некоторых элементарных алгебраических преобразований можно представить как:

_D =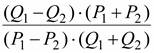

Именно этой формулой удобнее всего пользоваться при реальных вычислениях дуговой эластичности. Конечно, для этого необходимо знать числовые значения Q ₁, Q ₂ и P ₁, P ₂.

Дуговая эластичность может рассчитываться и для случая линейной функции спроса для любых ее отрезков.

2. Точечный метод. Представим теперь, что нам нужно определить эластичность не на отрезках ab и cd, а в некоторой произвольно взятой точке f на кривой спроса (рис. 2.11). В этом случае можно воспользоваться формулой 2.9, но заменив Q и Р бесконечно малыми величинами. Тогда эластичность можно определить как:

_D = 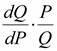(2.10)

Формула 2.10 показывает точечную эластичность спроса.

Точечная эластичность – это эластичность, измеренная в некоторой точке кривой.

dQ / dP – показывает изменение спроса в ответ на изменение цены. На рис. 2.11 – это тангенс угла, образуемый касательной к кривой спроса в точке f и осью ординат (tg). Он равен –70/50 = 1,44 (знак минус обусловлен отрицательным наклоном кривой спроса и, соответственно, касательной к ней). Относительно точки f P _f = 25, а Q _f = 35. Подставляем эти значения в формулу 2.10 и получаем, что _D = 1,44 (25/35) = 1,0. Следовательно, выше этой точки по кривой спроса спрос неэластичен, ниже – эластичен.

При изучении эластичности необходимо особо обратить внимание на то, что она лишь частично определяется наклоном кривой спроса. Это можно легко заметить на примере линейной функции спроса. С этой целью выберем знакомую нам функцию спроса Q _D = 60 4P и изобразим ее на рис. 2.12.

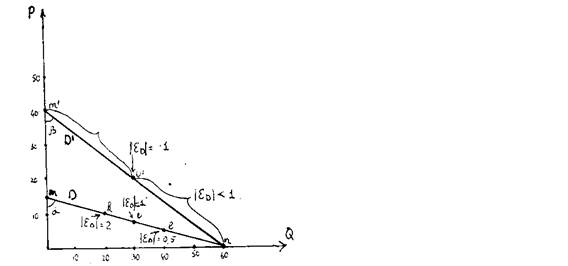
Рис. 2.12. Различные эластичности линейных функций спроса.

Очевидно, что у линейной функции угол наклона во всех ее точках одинаков. В нашем случае dQ / dP = tg = 4 на всем ее протяжении. Однако в разных ее точках значение ценовой эластичности будет различным в зависимости от выбранных значений Р и Q. Так, например, в точке k эластичность равна 2, а в точке l уже только 0,5. В точке u, которая делитлинию спроса mn ровно пополам, эластичность составляет 1.

Теперь предположим, что спрос возрос так, что линия спроса сместилась в положение mn. Она теперь описывается функцией Q _D = 60 1,5P. Хорошо видно, что угол ее наклона существенно изменился. Здесь dQ / dP = tg = 1,5. Однако, например, в точке u эластичность спроса равна 1, как и в точке u на линии спроса mn.

Заметим, что в точке, которая делит прямую линию спроса пополам, эластичность всегда равна – 1. На отрезке выше этой точки спрос в любой точке эластичный, ниже неэластичный в любой точке. Эти утверждения можно легко доказать, зная формулу определения эластичности и элементарную геометрию.

До сих пор мы стремились показать, что значения ценовой эластичности спроса различны для различных участков и точек линии, представляющих одну и ту же функцию спроса. Однако можно указать на три исключения, когда эластичность одинакова для всей кривой спроса. Во-первых, нетрудно заметить, что когда последняя представлена вертикальной прямой линией (рис. 2.13, график А), то эластичность спроса равна 0 (т.к. dQ / dP = 0). Такой спрос называют абсолютно неэластичным.

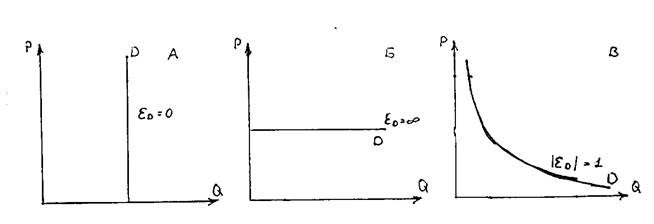
Рис. 2.13. Графики функций спроса с постоянными эластичностями.

Во-вторых, если кривая спроса представлена горизонтальной прямой линией (рис. 2.13, график Б), то эластичность спроса равна бесконечности (т.к. dQ / dP = 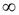). Такой спрос называют абсолютно эластичным.

И, наконец, в-третьих, когда кривая спроса представлена правильной гиперболой (рис. 2.13, график В), т.е. Q _D = 1/ P. Используя формулу 2.10 можно установить, что ее эластичность постоянна и равна 1, т.е. _D = 1.