Пусть F 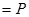 i
i 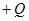 j
j 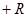 k – векторное поле, заданное в некоторой области
k – векторное поле, заданное в некоторой области 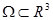 , и функции
, и функции 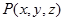 ,
, 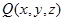 ,
, 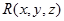 – непрерывно дифференцируемые в области
– непрерывно дифференцируемые в области 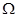 . Пусть L – гладкая кривая, расположенная в области
. Пусть L – гладкая кривая, расположенная в области 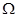 .
.
Криволинейный интеграл
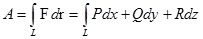
| (4) |
называется работой векторного поля F вдоль кривой L.
В случае если L – замкнутая кривая, то криволинейный интеграл (4) называется циркуляцией векторного поля F вдоль кривой L.
Таким образом, циркуляция поля F равна:
Ц 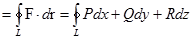 .
.
В случае когда векторное поле F  – плоское, его циркуляция вдоль замкнутой кривой L задается интегралом:
– плоское, его циркуляция вдоль замкнутой кривой L задается интегралом:
Ц 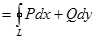 .
.
 2015-04-30
2015-04-30 710
710








