Теорема (Стокс). Пусть 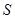 – гладкая ориентируемая поверхность, а L – замкнутая гладкая кривая, являющаяся границей поверхности
– гладкая ориентируемая поверхность, а L – замкнутая гладкая кривая, являющаяся границей поверхности 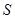 . Пусть n
. Пусть n 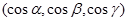 – единичная нормаль к поверхности
– единичная нормаль к поверхности 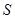 , задающая одну из ее сторон. Пусть векторное поле F
, задающая одну из ее сторон. Пусть векторное поле F 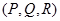 – непрерывно дифференцируемо на
– непрерывно дифференцируемо на 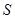 и L. Тогда
и L. Тогда
  | (5) |
причем направление обхода контура L выбрано так, что при взгляде с конца вектора n оно происходит против часовой стрелки.
Левый интеграл в формуле (5) представляет собой циркуляцию векторного поля F вдоль контура L, а правый – поток ротора этого поля через поверхность 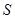 . Поэтому формулу Стокса удобно записывать в векторной форме:
. Поэтому формулу Стокса удобно записывать в векторной форме:
 rot F·n
rot F·n  (rot F)n
(rot F)n 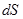 ,
,
т.е. поток ротора векторного поля F через ориентированную поверхность 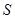 равен циркуляции поля F вдоль контура L этой поверхности (проходимого в положительном направлении).
равен циркуляции поля F вдоль контура L этой поверхности (проходимого в положительном направлении).
В случае, когда векторное поле F  – плоское, формула Стокса принимает вид формулы Грина:
– плоское, формула Стокса принимает вид формулы Грина:
 .
.
Формулу Стокса применяют для вычисления циркуляции векторного поля. Однако следует помнить, что для того, чтобы можно было применить формулу Стокса к контуру  , необходимо, чтобы область
, необходимо, чтобы область 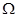 , в которой лежит
, в которой лежит 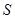 была поверхностно односвязной.
была поверхностно односвязной.
Область 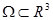 называется поверхностно односвязной, если для любого замкнутого контура
называется поверхностно односвязной, если для любого замкнутого контура  , найдется поверхность
, найдется поверхность  , границей которого является контур L.
, границей которого является контур L.
Пример 1. Найти циркуляцию плоского векторного поля F  по замкнутой кривой L в положительном направлении:
по замкнутой кривой L в положительном направлении:
а) F  , L – окружность, задаваемая уравнением
, L – окружность, задаваемая уравнением
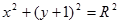 ;
;
б) F 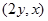 , L – контур треугольника
, L – контур треугольника 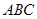 , где
, где  ,
,  ,
, 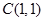 .
.
Решение. а) Запишем параметрические уравнения окружности:  ,
, 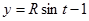 ,
,  . Находим
. Находим  ,
,  .
.
Тогда циркуляция поля F вдоль кривой L будет равна:
Ц 
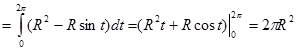 .
.
б) Первый способ.
Контур L есть объединение отрезков  ,
,  и
и  . Поэтому циркуляция поля F вдоль кривой L будет равна:
. Поэтому циркуляция поля F вдоль кривой L будет равна:
Ц  .
.
Вычислим каждый из интегралов. Вдоль отрезка  имеем
имеем 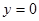 и, стало быть,
и, стало быть, 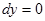 . Следовательно,
. Следовательно,
 .
.
Вдоль отрезка  имеем
имеем 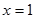 и
и  . Поэтому
. Поэтому
 .
.
И вдоль отрезка  имеем
имеем  и
и 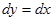 . Следовательно,
. Следовательно,

Таким образом, циркуляция поля F вдоль контура L будет равна: Ц 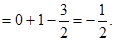
Второй способ.
Вычислим циркуляцию, применив формулу Грина:
Ц  ,
,
где областью D является треугольник 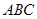 . В нашем случае
. В нашем случае  ,
, 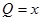 . Следовательно,
. Следовательно,  ,
,  . Тогда циркуляция поля F вдоль контура L будет равна
. Тогда циркуляция поля F вдоль контура L будет равна
Ц 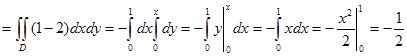 .
.
Пример 2. Вычислить циркуляцию пространственного векторного поля F  i
i  j
j 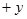 k вдоль эллипса L, получающегося пересечением цилиндра
k вдоль эллипса L, получающегося пересечением цилиндра 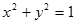 с плоскостью
с плоскостью  (при взгляде с положительного направления оси
(при взгляде с положительного направления оси 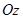 обход контура L совершается против часовой стрелки).
обход контура L совершается против часовой стрелки).
Первый способ.
Запишем параметрические уравнения эллипса:  ,
, 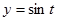 ,
, 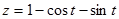 . При изменении параметра
. При изменении параметра  от
от  до
до  получаем требуемое направление обхода контура L. Вычислим теперь циркуляцию:
получаем требуемое направление обхода контура L. Вычислим теперь циркуляцию:
Ц 
 .
.
Второй способ.
Вычислим циркуляцию, применив формулу Стокса, причем в качестве поверхности 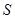 , ограничиваемой кривой L, выберем часть плоскости
, ограничиваемой кривой L, выберем часть плоскости  , лежащей внутри цилиндра
, лежащей внутри цилиндра 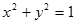 . Единичную нормаль к плоскости выберем так, чтобы, глядя с ее конца, направление обхода контура L проходило против часовой стрелки. Такой единичной нормалью будет вектор n
. Единичную нормаль к плоскости выберем так, чтобы, глядя с ее конца, направление обхода контура L проходило против часовой стрелки. Такой единичной нормалью будет вектор n  . По формулу Стокса имеем:
. По формулу Стокса имеем:
Ц  rot F·n
rot F·n 

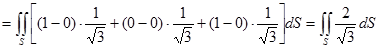 .
.
Вычисление последнего интеграла сведем вычислению двойного интеграла по области 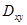 , являющейся проекцией поверхности
, являющейся проекцией поверхности 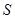 на плоскость
на плоскость  . Этой областью будет круг
. Этой областью будет круг 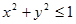 . Поскольку
. Поскольку  , то окончательно получаем:
, то окончательно получаем:
Ц=  .
.
Контрольные вопросы:
- Дайте определение работы векторного поля F вдоль кривой L.
- Дайте определение циркуляции векторного поля F вдоль кривой L.
- Приведите формулу Стокса.
- Дайте определение поверхностно односвязной области.
 2015-04-30
2015-04-30 6214
6214
