Оператор Гамильтона или оператор 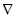 (набла) определяется формулой
(набла) определяется формулой
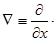 i
i 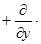 j
j 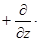 k.
k.
Применение этого оператора к скалярным и векторным полям с формальной точки зрения соответствует операции «умножения» на вектор с координатами 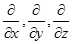 :
:
 i
i 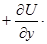 j
j 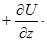 k,
k,
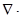 F
F 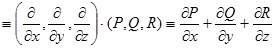 ,
,
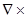 F
F 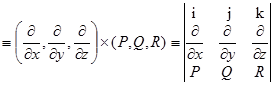 .
.
Нетрудно заметить, что стоящие в правых частях последних трех равенств выражения суть градиент, дивергенция и ротор полей:
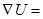 grad
grad 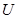 ,
, 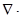 F
F 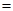 div F,
div F, 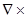 F
F 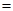 rot F.
rot F.
Пример. Вычислить дивергенцию и ротор векторного поля
F 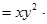 i
i 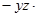 j
j 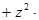 k.
k.
По определению, div F 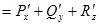 . В нашем случае
. В нашем случае 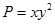 ,
, 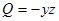 ,
, 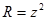 . Отсюда находим
. Отсюда находим  ,
, 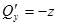 ,
, 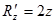 . Следовательно,
. Следовательно,
div F 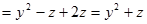 .
.
Вычислим ротор поля F:
rot F 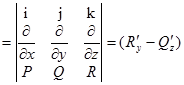 i
i 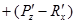 j
j 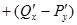 k
k 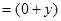 i
i 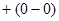 j
j 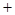
 k
k 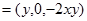 .
.
Контрольные вопросы:
- Дайте определение дивергенции векторного поля F
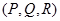 .
. - Дайте определение ротора векторного поля F
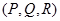 .
. - Какой формулой определяется оператор Гамильтона?
 2015-04-30
2015-04-30 659
659








