2015-04-30
1193
Пусть в области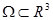 
задано некоторое векторное поле F 
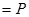i 
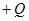j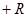 
k, где 
, 
, 
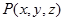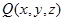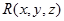– непрерывно дифференцируемые в области 
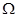функции. Пусть 
– гладкая ориентируемая поверхность, на которой выбрана определенная сторона, задаваемая единичной нормалью n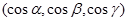 
к этой поверхности.
Потоком векторного поля F через поверхность S в направлении единичной нормали n называют поверхностный интеграл первого рода:
П  .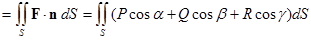
| (1) |
Поверхностный интеграл первого рода в формуле (1) связан с поверхностным интегралом второго рода равенством:
П  ,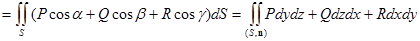
| (2) |
которое дает еще один способ вычисления потока.
Физический смысл потока: если вектор-функция F есть поле скоростей текущей жидкости, то поток П этого векторного поля через поверхность S общему количеству жидкости, протекающей через S за единицу времени.
