Принятие решений в условиях неопределенности
Нередко при решении экономических задач возникает необходимость выбора оптимального решения в условиях неопределенности и риска. Особенностью таких условий является неясность исходов, последствий выбора решений одной стороной под влиянием случайных факторов и неизвестность поведения противоположной стороны. Такие ситуации называются играми с природой (иногда статистическими играми). Они решаются с помощью методов теории статистических решений. Термин «природа» характеризует некоторую объективную действительность, которая выступает как не имеющий конкретной цели и случайным образом выбирающий очередные ходы партнер по игре. Природа безразлична к выигрышу.
Сторона, принимающая решение (игрок А или статистик), имеет т стратегий: А1, А2, …, Аm. Природа может реализовать n возможных состояний: П1 П2, …, Пn. Поскольку природа не является заинтересованной стороной, исход любого сочетания поведения сторон можно оценить с помощью выигрышей 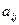 игрока А для каждой пары стратегий Аi, и Пj. Все показатели игры записываются в виде платежной матрицы.
игрока А для каждой пары стратегий Аi, и Пj. Все показатели игры записываются в виде платежной матрицы.
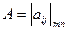
Часто построение платежной матрицы является наиболее трудоемким этапом подготовки принятия решения.
При анализе игры с природой вводится также показатель, позволяющий оценить, насколько то или иное состояние природы влияет на исход ситуации. Этот показатель называется риском.
Риском 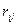 статистика, когда он пользуется чистой стратегией Аi; при состоянии Пj природы, называется разность между максимальным выигрышем
статистика, когда он пользуется чистой стратегией Аi; при состоянии Пj природы, называется разность между максимальным выигрышем 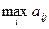 , который он мог бы получить, достоверно зная, что природой будет реализовано именно состояние Пj, и тем выигрышем
, который он мог бы получить, достоверно зная, что природой будет реализовано именно состояние Пj, и тем выигрышем 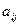 , который он получит, используя стратегию Аi, не зная, какое из состояний Пj природа действительно реализует. То есть элементы матрицы рисков определяются по формуле.
, который он получит, используя стратегию Аi, не зная, какое из состояний Пj природа действительно реализует. То есть элементы матрицы рисков определяются по формуле.
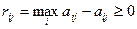
Решение статистической игры может находиться либо в смешанных стратегиях, либо в чистых стратегиях.
Учитывая специфику статистических игр, при поиске оптимальных решений обращаются к различным критериям, дающим некоторую логическую схему принятия решения. Поскольку критерии формулируются на основе здравого смысла, интуиции и практической целесообразности, то они помогают оценить принимаемое решение с различных позиций, что позволяет избежать грубых ошибок в хозяйственной деятельности.
Применяется две группы критериев — использующих и не использующих априорные вероятности 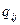 состояний природы. К первой группе относятся критерии Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимается чистая стратегия А;, при которой максимизируется средний выигрыш статистика
состояний природы. К первой группе относятся критерии Байеса и Лапласа. В качестве оптимальной по критерию Байеса принимается чистая стратегия А;, при которой максимизируется средний выигрыш статистика
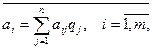
то есть обеспечивается
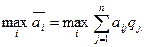
Если статистику представляются в равной мере правдоподобными все состояния Пj природы, то
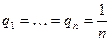
и оптимальной по критерию Лапласа считается чистая стратегия Аi, обеспечивающая
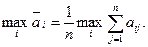
Ко второй группе критериев, применяемых при неизвестных априорных вероятностях состояний природы, относятся критерии Вальда, Сэвиджа и Гурвица. Оптимальной по критерию Вальда считается чистая стратегия Аi, при которой наименьший выигрыш статистика будет максимальным, то есть ему обеспечивается
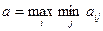 .
.
Для смешанных стратегий критерий Вальда формулируется так: оптимальной считается та смешанная стратегия, при которой минимальный средний выигрыш статистика 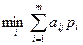 , будет максимальным, то есть стратегия p *, найденная из условия
, будет максимальным, то есть стратегия p *, найденная из условия
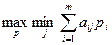 .
.
Оптимальной по критерию Сэвиджа считается та чистая стратегия Аi при которой минимизируется величина r i максимального риска, то есть обеспечивается 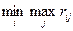 .
.
Для смешанных стратегий критерий Сэвиджа формулируется так: оптимальной считается та смешанная стратегия, при которой максимальный средний риск статистика 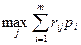 минимизируется, то есть стратегия р*, найденная из условия
минимизируется, то есть стратегия р*, найденная из условия 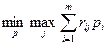
Оптимальной по критерию Гурвица считается чистая стратегия Ai, найденная из условия
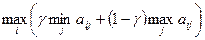 ,
,
где г принадлежит интервалу (0; 1) и выбирается из субъективных соображений.
При г = 1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда, а при г = 0 — в критерий крайнего оптимизма.
Надо отметить, что анализ практических ситуаций следует проводить по нескольким критериям, что позволит глубже вникнуть в суть явления и выбрать обоснованное решение.
Решение матричных игр сведением к задаче линейного программирования
Пусть игра задана платежной матрицей.
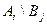
| 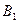
| 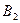
| … | 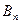
|
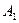
| 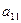
| 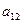
| … | 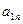
|
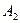
| 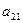
| 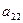
| … | 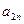
|
| … | … | … | … | |
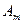
| 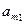
| 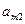
| … | 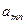
|
Оптимальные смешанные стратегии 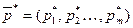 и
и 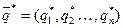 игроков А и В могут быть найдены в результате решения пары двойственных задач линейного программрования.
игроков А и В могут быть найдены в результате решения пары двойственных задач линейного программрования.
Для игрока А:
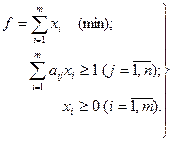
В результате решения задачи находятся оптимальный вектор 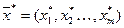 и
и 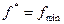 , а затем
, а затем 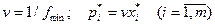 .
.
Для игрока В:
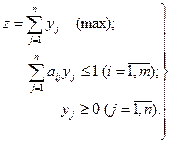
Решая задачу, находят оптимальный вектор 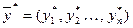 и
и 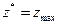 , а затем
, а затем 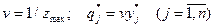 .
.
 2015-04-30
2015-04-30 445
445








