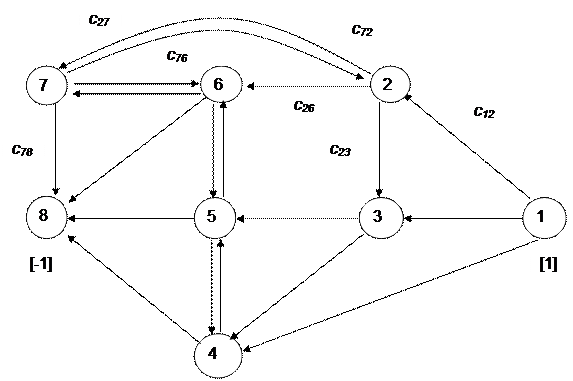
Общие сведения. Пусть некоторая сеть задана в виде орграфа (рис

Пусть некоторая сеть задана в виде орграфа (рис. 1), т.е. каждой ориентированной дуге соответствует определенное расстояние. Необходимо найти кратчайший путь из i -го узла сети в ее заданный j -й узел. К этой задаче, известной в исследовании операций как задача выбора кратчайшего пути, сводятся такие практически важные задачи, как задача о замене оборудования, задача о календарном планировании комплекса работ и т.д.

c₆₅

c₁₃

c₄₅

c₁₄

Рис. 1

Как правило, в сети выделяют один узел, который является конечным (пункт или станция назначения, сток). Задача заключается в отыскании кратчайшего пути в этот конечный узел (на рис. 1 конечным является узел с номером 8) из некоторого другого узла сети (например, из первого узла сети на рис. 1). Величина c_ij определяет расстояние от i -го узла сети до ее j -го узла.

Величина с_ij может измеряться в единицах, отличных от единиц длины. Так, например, c_ij может представлять собой стоимость проезда от i -го до j -го узла сети. Тогда задача заключается в отыскании пути минимальной стоимости. Величина c_ij может также определять время переезда от i -го до j -го узла сети. При этом необходимо найти путь с минимальной продолжительностью переезда.

При решении прикладных задач, сводящихся к задаче выбораа кратчайшего пути, часто встречаются ситуации, когда c_ij ¹ c_ji. Кроме того, как правило, не выполняется так называемое неравенство треугольника: c_ij £ c_ik + c_kj для всех некоторых значений индексов i, j, k.

Существуют сети, содержащие циклы, каждый из которых представляет собой замкнутый путь (путь, исходящий из некоторого узла сети и возвращающийся в него же). Так, в сети представленной на рис. 1, много циклов, один из них содержит узлы с номерами 2, 3, 5, 6 и 7. Как правило, в задачах исследования операций значения c_ij положительны и общая длина цикла является положительной. Следовательно, решение задачи выбора кратчайшего пути не может содержать циклов.

Предположим, что для сети, представленной на рис. 1, необходимо найти кратчайший путь от узла с номером 1 (источник) до узла с номером 8 (сток). Установим связь этой задачи с классической транспортной задачей.

Рассмотрим транспортную задачу с промежуточными пунктами, сеть которой представлена на рис. 1. При этом предположим, что: а) в узле с номером 1 имеется избыточная единица товара; б) в узле с номером 8 имеется недостаток единицы товара; в) узлы с номерами 2,...,7 являются промежуточными пунктами с нулевыми чистыми запасами (потребность в дополнительных поставках товара равна нулю). Необходимо разработать план перевозок товара между узлами сети (складами), который при минимальных транспортных затратах позволит на каждом складе поддерживать нулевой чистый запас товара.

Считаем, что каждой ориентированной дуге сети соответствует переменное модели x_ij, представляющее собой количество товара, которое должно быть отправлено с i -го склада на j -й. Для каждого k -го промежуточного пункта вводим переменное x_kk с соответствующим ему коэффициентом c_kk = 0 в целевой функции, а величину чистого запаса обозначаем через T_k. Если множество пар индексов (i, j), соответствующих ориентированным дугам сети, представленной на рис. 1, обозначить через J, то рассматриваемую задачу можно записать следующим образом: