2015-04-20
192
Пусть изучается ряд (1)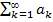 
с положительными членами. Рассмотрим 
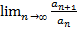. Предположим, что данный предел существует и равен 
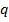. Тогда при
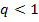ряд (1) сходится,
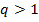ряд (1) расходится,
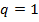ответа нет.
Доказательство. Пусть 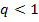. Возьмем некоторое число 
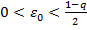, другими словами 
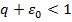. Для данного фиксированного числа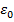 
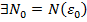, что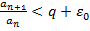 
, 
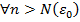. Тогда имеем, что
.
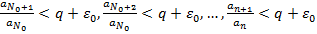Умножая все эти неравенства, получим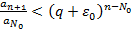 
. Это означает, что
.
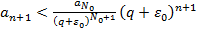Обозначим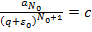 
, т.к. 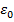и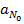 
фиксированы, то получим, что
.
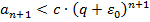Сравним ряды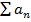 
и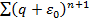 
, для них работает теория сравнения
Т.к. 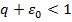, то 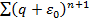сходится, следовательно сходится и .
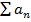Аналогично доказывается случай, когда (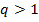
, 
).
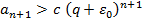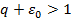Примеры:
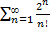
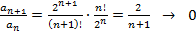
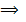ряд сходится,
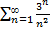
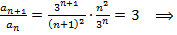ряд расходится.
При 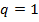-ответ нет, т.к. если рассмотреть ряды
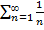
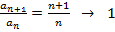расходится,
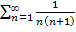
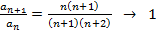сходится.
Замечание: 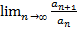может не существовать. Тогда употребляется следующий признак: если 
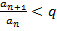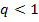и при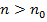 
ряд сходится; если 
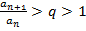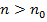, - ряд расходится.
