2015-04-20
628
Установить сходимость ряда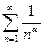 
, 
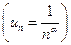ни по признаку Коши, ни по признаку Д’Аламберa невозможно т.к. если применить Признак Д ’ Аламбера: 
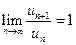, если применить Радикальный признак Коши: предел 
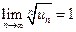, в обоих случаях ответа (относительно сходимости ряда) нет.
Докажем теперь признак, с помощью которого можно проверить сходимость гармонических рядов.
Интегральный признак Коши. Если функция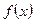 
неотрицательна и убывает на промежутке 
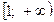, то ряд 
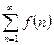и несобственный интеграл 
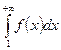сходятся или расходятся одновременно.
Доказательство. Так как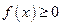 
и 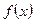монотонно убывающая функция, то для любого 
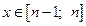имеем 
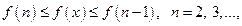т.е.
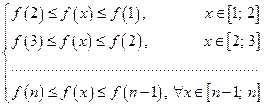
Суммируя эти неравенства и учитывая, что
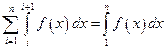имеем
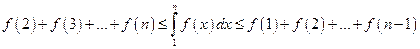или
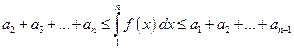
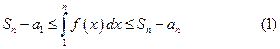
С помощью неравенства (1) докажем эквивалентность сходимости ряда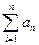 
и интеграла 
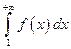. Пусть 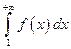сходится. Отсюда следует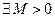, что 
, что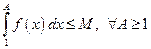 
. В частности для любого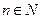 
.
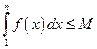Из левой части неравенства (1) имеем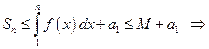 
частичные суммы 
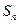положительного ряда ограничены числом 
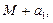т.е. ряд сходится, тогда 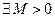, что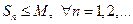 
. Берем 
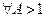и рассмотрим
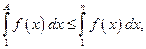где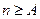 
натуральное число. Тогда из правой части неравенства (1) имеем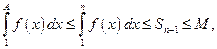 
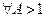
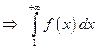интеграл сходится. Теорема доказана.
