- При
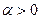 функция
функция 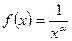 неотрицательна и убывает на промежутке
неотрицательна и убывает на промежутке 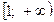 . Интеграл
. Интеграл 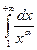 сходится при
сходится при 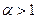 и расходится при
и расходится при 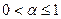 . Поэтому ряд
. Поэтому ряд 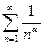 сходится при
сходится при 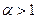 и расходится при
и расходится при 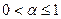 .
. - При
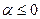 ряд
ряд 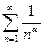 расходится, так как в этом случае
расходится, так как в этом случае 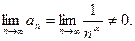
Итак, ряд 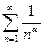
ü сходится при 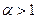 и
и
ü расходится при 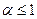 .
.
Сходимость знакопеременных рядов
Определение. Ряды типа 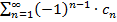 (1).
(1). 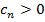 называется знакопеременными (знакочередующимися).
называется знакопеременными (знакочередующимися).
Теорема Лейбница. Если в знакопеременном ряде (1), 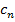 монотонно убывающим образом стремится к 0, т.е.
монотонно убывающим образом стремится к 0, т.е. 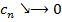 , то ряд (1) сходится.
, то ряд (1) сходится.
Доказательство. Рассмотрим частичные суммы данного ряда: 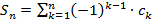 .
.
Изучим 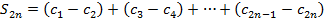 и рассмотрим каждое из этих слагаемых
и рассмотрим каждое из этих слагаемых 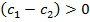 ,
, 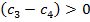 ,
, 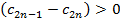 ,
,
Покажем, что 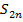 монотонно
монотонно 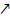 . Сравним
. Сравним 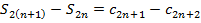 , т.к.
, т.к.
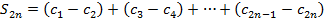
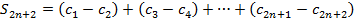 .
.
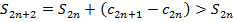 , т.е.
, т.е.
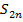 монотонно возрастающая последовательность.
монотонно возрастающая последовательность.
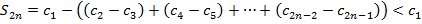 т.е.
т.е.
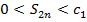 .
.
Отсюда, 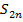 - монотонно
- монотонно 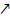 последовательность и
последовательность и 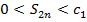 . Следовательно,
. Следовательно, 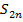 сходится к некоторому числу
сходится к некоторому числу 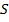 при
при 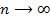 . Рассмотрим нечетную последовательность
. Рассмотрим нечетную последовательность
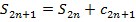 . Так как
. Так как 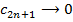 , а
, а 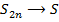
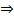
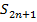 сходится и сходится к числу
сходится и сходится к числу 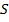 , т.к.
, т.к. 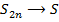 ,
, 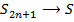 , тогда последовательность
, тогда последовательность 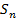 сходится и сходится к элементу
сходится и сходится к элементу 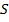 ,
, 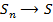 , что и т.д.
, что и т.д.
Если изучить ряд 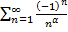 в частности при
в частности при 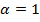 получаем
получаем 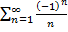 ,
, 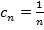 и который
и который
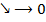 . Получаем
. Получаем 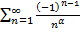 сходится если
сходится если 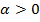 , то
, то 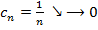 и получаем
и получаем 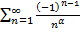 при
при 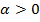 сходится.
сходится.
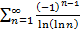
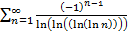
11. Сходимость произвольных рядов
Пусть имеем ряд 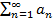 (1), где
(1), где 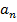 - произвольные действительные числа. Параллельно с ним рассмотрим ряд
- произвольные действительные числа. Параллельно с ним рассмотрим ряд 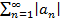 (2).
(2).
Определение. Ряд (1) абсолютно сходится, если ряд (2) сходится. Сходимость ряда (2) проверить легко, т.к. это уже ряд с положительными членами, а это уже было рассмотрено.
Например: 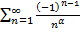 , т.к.
, т.к. 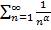 при
при 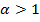 сходится, то
сходится, то 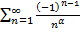 при
при 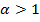 абсолютно сходится. А если
абсолютно сходится. А если 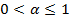 , то
, то 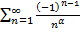 будет сходиться, но не абсолютно.
будет сходиться, но не абсолютно.
Теорема. Если ряд абсолютно сходится, то данный ряд сходится.
Доказательство. Рассмотрим 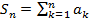 и
и 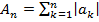 . Знаем, что
. Знаем, что 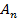 сходится. Это значит, что
сходится. Это значит, что 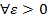 ,
, 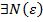 , что
, что 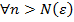 и
и 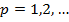
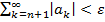 . Для данных
. Для данных 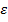 ,
, 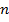 ,
, 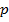 рассмотрим
рассмотрим 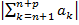 . По неравенству треугольника
. По неравенству треугольника 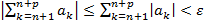 ,
, 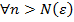 .
.
Обратное неверно, т.е. если рассмотреть ряд 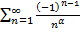 при
при 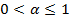 , он сходится, но абсолютно не сходится.
, он сходится, но абсолютно не сходится.
Степенные ряды Тейлора
Определение. Степенным рядом называется следующий ряд 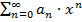 (1), т.е. общий член ряда не число, а функция
(1), т.е. общий член ряда не число, а функция 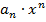 . Если зафиксировать некоторое число
. Если зафиксировать некоторое число 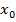 , то получается числовой ряд и можно говорить уже о сходимости или абсолютной сходимости.
, то получается числовой ряд и можно говорить уже о сходимости или абсолютной сходимости.
Обозначим через 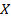 множество всех
множество всех 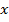 -ов из
-ов из 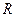 для которых (1) сходится. Изучим характер множества
для которых (1) сходится. Изучим характер множества 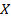 . Степенные ряды удовлетворяют следующему свойству:
. Степенные ряды удовлетворяют следующему свойству:
Теорема Абеля. Если в некоторой точке 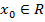 ряд (1) сходится, то для
ряд (1) сходится, то для 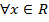
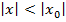 ряд будет сходится абсолютно.
ряд будет сходится абсолютно.
Доказательство. Знаем, что 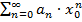 сходится
сходится 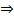
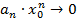
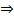 данная последовательность ограничена, т.е.
данная последовательность ограничена, т.е. 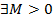 , что
, что 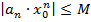 для
для 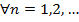 .
.
Изучим на абсолютную сходимость следующий ряд 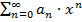 . Для этого оценим общий член
. Для этого оценим общий член 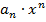 .
.
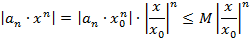
Получим, что 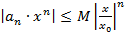 . Имеем также
. Имеем также 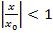 . Используем теорему о сравнении, сравним ряды
. Используем теорему о сравнении, сравним ряды 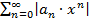 и
и 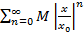 . Т.к.
. Т.к. 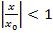 , то ряд сходится и по теореме о сравнении I-ый ряд тоже сходится. Следовательно, ряд (1) сходится, притом абсолютно.
, то ряд сходится и по теореме о сравнении I-ый ряд тоже сходится. Следовательно, ряд (1) сходится, притом абсолютно.
 Из теоремы Абеля следует, что если для некоторой точки
Из теоремы Абеля следует, что если для некоторой точки 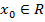 ряд (1) сходится, то в окрестности
ряд (1) сходится, то в окрестности 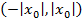 ряд (1) опять сходится.
ряд (1) опять сходится.
Это подсказывает, что множество 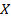 представляет собой интервал. Заметим, что ряд (1) всегда сходится в точке 0.
представляет собой интервал. Заметим, что ряд (1) всегда сходится в точке 0.
Справедлива следующая теорема
Теорема. Если ряд (1) не везде сходится или расходится, то обязательно существует такое число 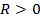 , для
, для 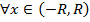 , т.е.
, т.е. 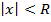 ряд (1) сходится, а для
ряд (1) сходится, а для 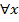
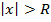 ряд (1) расходится.
ряд (1) расходится.
Доказательство. Как отметили множество 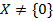 и множество
и множество 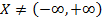 . Это значит, что
. Это значит, что 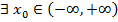 , где ряд (1) расходится. Тогда по теореме Абеля для
, где ряд (1) расходится. Тогда по теореме Абеля для 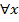 ,
, 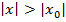 ряд (1) расходится. Это значит, что множество
ряд (1) расходится. Это значит, что множество 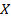 находится внутри интервала
находится внутри интервала 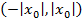 .
.

Значит, множество 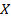 ограниченное множество, а мы знаем, что для ограниченного множества существует конечный
ограниченное множество, а мы знаем, что для ограниченного множества существует конечный 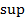 . Обозначим
. Обозначим 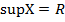 . Докажем, что
. Докажем, что 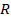 - это число, которое нам нужно, т.е. внутри интервала
- это число, которое нам нужно, т.е. внутри интервала 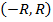 ряд (1) сходится, вне интервала – расходится. Возьмем
ряд (1) сходится, вне интервала – расходится. Возьмем 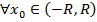 .По определению
.По определению 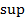 , т.к.
, т.к. 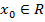 обязательно
обязательно 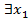 , такой, что
, такой, что 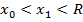 ,
, 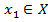 . А если такой элемент
. А если такой элемент 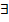 , тогда можно сказать, что по теореме Абеля, если в точке
, тогда можно сказать, что по теореме Абеля, если в точке 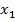 ряд (1) сходится и
ряд (1) сходится и 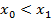 , то в точке
, то в точке 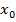 ряд (1) тоже сходится, т.е. мы показали, что внутри
ряд (1) тоже сходится, т.е. мы показали, что внутри 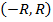 ряд (1) сходится. Пусть теперь
ряд (1) сходится. Пусть теперь 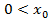 и
и 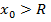 . Тогда можно сказать, что
. Тогда можно сказать, что 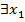 , что
, что 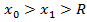 ,
, 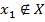 . По теореме Абеля, если
. По теореме Абеля, если 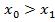 , в точке
, в точке 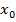 ряд расходится, что и т.д.
ряд расходится, что и т.д.
Замечание. Мы показали, что 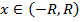 и может быть сюда будут входить концевые точки, т.е.
и может быть сюда будут входить концевые точки, т.е. 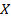 представляет из себя интервал, который называется интервалом сходимости степенного ряда, а
представляет из себя интервал, который называется интервалом сходимости степенного ряда, а 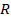 называется радиусом сходимости степенного ряда.
называется радиусом сходимости степенного ряда.
Добавим крайний случай: если 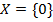 тогда предположим, что
тогда предположим, что 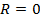 , а если
, а если
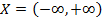 , то предположим, что
, то предположим, что 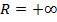 .
.
Следовательно, 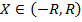 в любом случае. Значит вопрос об изучении сходимости степенного ряда сводится к нахождению радиуса сходимости.
в любом случае. Значит вопрос об изучении сходимости степенного ряда сводится к нахождению радиуса сходимости.
Для нахождения радиуса сходимости справедлива следующая теорема
Теорема. Пусть 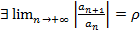 . Тогда при
. Тогда при
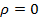
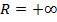 ,
,
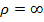
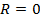 ,
,
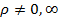
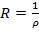 .
.
Доказательство. Пусть 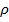 конечное и
конечное и 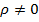 . Обозначим через
. Обозначим через 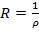 и докажем, что
и докажем, что 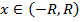 ряд (1) сходится, а для произвольного
ряд (1) сходится, а для произвольного 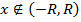 ряд (1) расходится.
ряд (1) расходится.
Пусть число 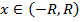 и фиксированное, тогда ряд (1) – числовой ряд. Для сходимости применим признак Даламбера. Изучим
и фиксированное, тогда ряд (1) – числовой ряд. Для сходимости применим признак Даламбера. Изучим 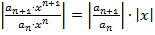
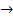
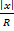 . По признаку Даламбера, если
. По признаку Даламбера, если 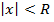 , то ряд (1) сходится, если
, то ряд (1) сходится, если 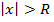 , то ряд (1) расходится. При
, то ряд (1) расходится. При 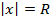 ответа нет.
ответа нет.
Замечание. Так как 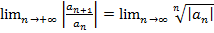 , то радиус сходимости можно посчитать по формуле
, то радиус сходимости можно посчитать по формуле 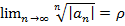
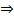
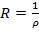 . Эта формула называется формулой Коши-Адамара.
. Эта формула называется формулой Коши-Адамара.
Примеры:
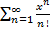
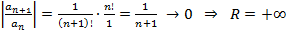
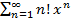
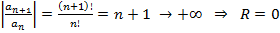
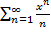
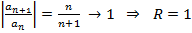
ряд сходится в 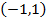 и расходится вне
и расходится вне 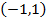 .
.
Проверим в 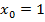
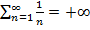 расходится
расходится
в 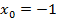
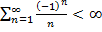 сходится.
сходится.
Следовательно 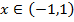 .
.
Свойства степенных рядов
(1) 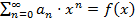
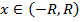
Теорема 1. Если степенной ряд сходится к некоторой функции 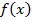 , то функция
, то функция 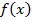 имеет производную любого порядка в интервале
имеет производную любого порядка в интервале 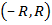 и
и 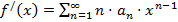
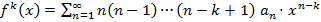 .
.
Доказательство. Рассмотрим степенной ряд 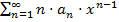 . Если радиус сходимости ряда (1)
. Если радиус сходимости ряда (1) 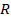 , то радиус сходимости этого ряда тоже
, то радиус сходимости этого ряда тоже 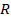 , т.к.
, т.к.
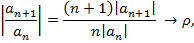
т.е. радиусы сходимости не нарушаются.
Теорема 2. Для 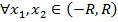
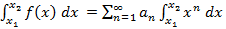 .
.
Если интегрировать, в частности, 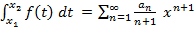 , радиус которого опять
, радиус которого опять 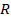 .
.
Исходя из этих свойств, пусть степенной ряд сходится к функции 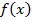 . Можно вычислить коэффициент
. Можно вычислить коэффициент 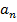 . Имеем:
. Имеем:
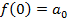
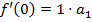
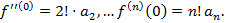
Следовательно, 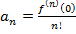 – это значит, что
– это значит, что 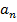 – коэффициенты Тейлора. Тем самым для функции
– коэффициенты Тейлора. Тем самым для функции 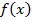 получаем разложение
получаем разложение
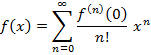
Ряд 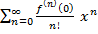 (2) называется рядом Тейлора или Маклорена.
(2) называется рядом Тейлора или Маклорена.
Возникает вопрос: Когда бесконечно дифференцируемая функция 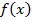 восстанавлевается своим рядом Тейлора? По формуле Тейлора имеем
восстанавлевается своим рядом Тейлора? По формуле Тейлора имеем
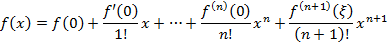
Обозначим 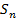 частичную сумму ряда (2) и обозначим
частичную сумму ряда (2) и обозначим
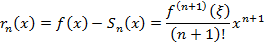
Получим условия: для того, чтобы функция 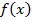 восстанавливалась рядом Тейлора (2) в
восстанавливалась рядом Тейлора (2) в 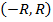 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 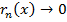 для
для 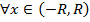 .
.
Примеры:
1. 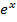
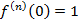 .
.
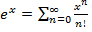
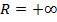
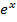 разлагается в степенной ряд в окрестности
разлагается в степенной ряд в окрестности 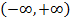 .
.
Если рассмотреть 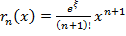 для любого фиксированного
для любого фиксированного 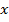 , т.к.
, т.к. 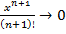 , то
, то 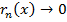
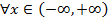 .
.
2. 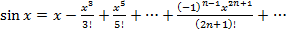 сходится в
сходится в 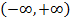 .
.
3. 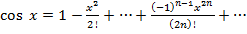 сходится в
сходится в 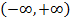 .
.
4. 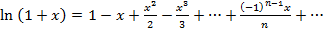
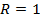 , сходится в
, сходится в 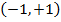 .
.
Рассмотрим при 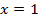 , получается
, получается 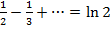 следует, что ряд сходиться в
следует, что ряд сходиться в 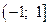
5. 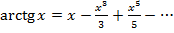
сходится в 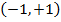 . В точке
. В точке 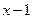 имеем
имеем 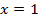
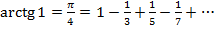
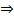
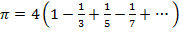 .
.
В концевых точках 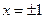 имеем знакопеременный ряд, который сходится.
имеем знакопеременный ряд, который сходится.
 2015-04-20
2015-04-20 263
263







