Признак Коши

Теорема. Пусть имеем ряд 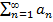(1), где 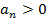. Рассмотрим 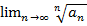. Пусть предел существует и равен 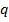. Тогда при

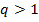
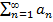- расходится,

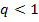
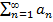- сходится,

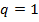ответа нет.

Доказательство. Допустим,что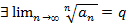

а) Пусть 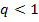. Рассмотрим 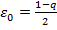. Тогда для данног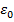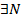о , что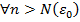

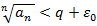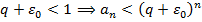, . Вспомним теорему о сравнении. Сравним ряд 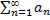с рядом 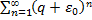. Второй ряд сходится, т.к. 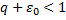и по теореме о сравнении следует, что первый ряд также сходится, что и т.д.

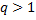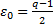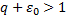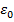
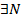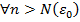
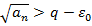
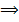
б) . Обозначим . Понятно, что . Для данного , что 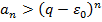. Сравним ряды 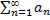и 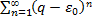, т.к. 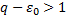, то II-ой из них расходится по теореме о сравнении расходится и I ряд.

в) 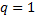. Если 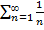понятно, что 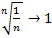, а мы знаем, что этот ряд расходится. Ряд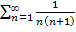 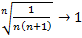, и мы знаем, что этот ряд сходится. Поэтому ответа нет, что и т.д.

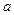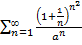Пример. При каких значениях ряд сходится?

По признаку Коши:

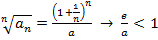, т.е. при

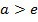ряд сходится,

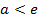ряд расходится,

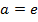ответа нет.

_______________________

Какой же из этих признаков сильней?

Показать, что если 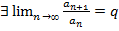(1), то 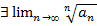(2) и они равны между собой, но обратное неверно.

_______________

Действительно,

рассмотрим ряд .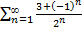

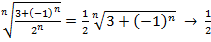сходится по Коши.

По Д’Аламберу имеем

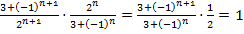при 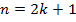и следовательно ответа нет.