Метод отделения корней

Метод отделения корней используется для определения интервалов, в которых содержатся корни уравнения. Это может быть сделано тремя способами.

1. Вычисляются значения функции 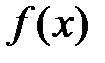в нескольких точках отрезка 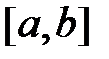и строится таблица. Если в двух соседних точках 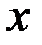функция имеет разные знаки, то корень уравнения находится между этими точками.

2. Строится график функции 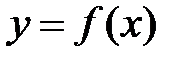и находятся точки пересечения его с осью абсцисс.

3. Исходная функция 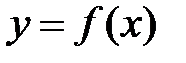представляется в эквивалентном виде 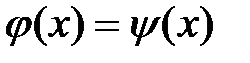. Строятся графики этих функций и находятся точки пересечения этих графиков.

На рис. 2.1 представлено окно программы, реализующей метод отделения корней тремя способами. Исходное уравнение .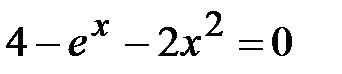

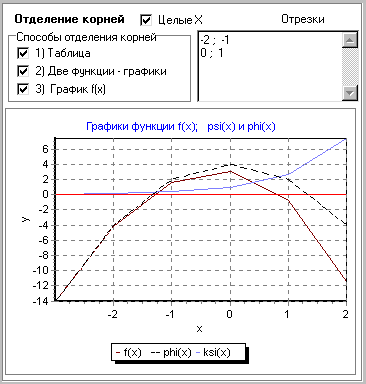
Рис. 2.1. Три способа отделения корней

1. Находя последовательно значения функции 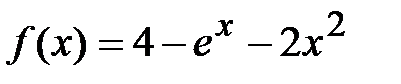для всех целых 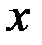на отрезке 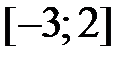и проверяя знак функции, выделим два отрезка, на которых функция меняет знак: 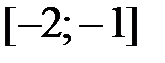и 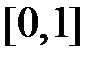(рис. 2.1, вверху справа).

2. Строится график функции 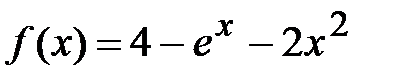и находятся точки его пересечения с осью абсцисс либо отрезки, содержащие точки пересечения.

3. Строятся графики функци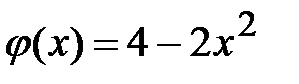й и 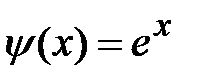и находятся точки их пересечения.