2015-04-20
532
Вариант 12
Для графа G=(X,U) (рисунок 1) выполнить следующее:
1.1. Построить:
- матрицу смежности;
- матрицу инцидентности.
1.2. Определить степени для всех вершин {xi} данного графа. 
Решение
Расставим метки вершин и ребер в графе. Получаем 9 вершин и 15 ребер.
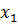
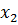
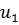
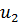
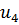
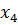
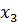
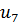
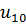
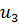
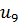
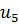
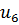
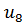
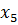
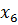
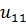
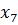
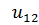
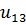
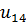
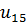
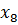
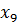
Построим матрицу смежности заданного графа, используя правило:
|
|
|
|
|
|
|
|
|
| |
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
|
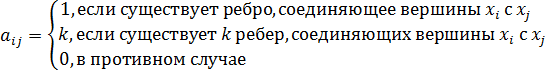
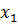
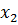
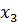
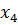
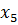
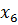
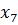
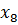
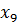
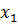
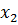
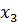
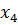
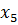
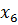
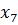
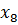
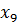
Построим матрицу инцидентности, используя правило:
|
|
|
|
|
|
|
|
|
| |
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
| |||||||||
|
| |||||||||
|
| |||||||||
|
| |||||||||
| |||||||||
|
| |||||||||
|
| |||||||||
|
|
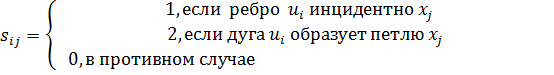
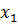
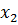
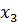
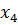
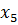
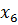
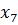
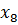
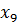
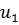
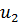
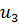
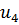
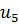
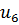
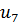
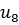
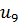
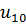
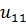
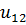
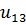
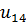
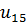
Определим степени вершин данного графа. Степень вершины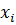 
равна количеству единиц в столбце матрицы инцидентности:
|
|
|
| 
| 
| 
| 
| 
| 
| 
| 
|
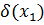
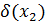
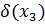
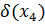
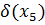
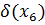
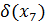
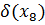
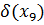
Задание 2.
По матрицам смежности А (рисунок 2) и инцидентности С (рисунок 3) построить графы G1 и G2.
Рисунок 2
Рисунок 3
Решение
 |
▪ 
▪ ▪ 
▪ ▪ ▪ 
▪
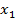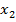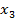
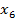
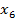
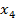
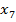граф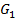 
4 5 1
7 6
граф 
Задание 3.
Для графа G=(X,U) (рисунок 1) построить кратчайшие маршруты, связывающие вершину, помеченную * (любую из двух), с остальными вершинами, указать их длину.
|
|
|
|
|
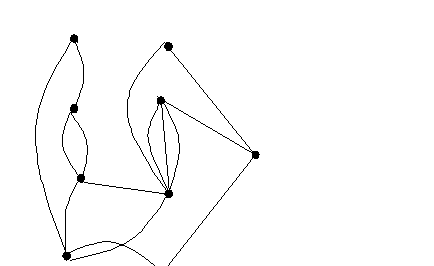Рисунок 1 
