2015-04-20
285
В заданном графе расставим произвольно номера вершин и длины (веса) ребер.
Вершину, помеченную звездочкой, сделаем первой и будем искать все кратчайшие пути от этой вершины до остальных, используя алгоритм Дейкстры.
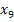
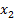
10 3 7 6
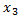
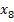4
2 1 2
2 2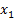 
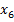
4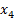 
7 8
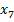
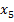
Найдем кратчайший путь от вершины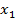 
до всех вершин графа. Вершинам графа будут присваиваться временные метки, которые затем по определенным правилам заменяются на постоянные. Будем использовать обозначения:
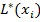– постоянная метка вершины 
;
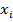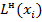– новая временная метка вершины ;
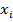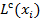– старая временная метка вершины ;
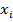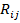- вес ребра, соединяющего вершины 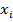с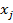 
.
Новая временная метка вычисляется по формуле:
.
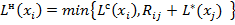Результаты действий на каждом шагу будем заносить в таблицу.
| Шаги | Вершины |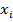
|
| |||||||||
|
| 
| 
| 
| 
| 
| 
| 
| 
| ||||
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
| ||||||||
|
|
|
| ||||||||||
|
|
|
| ||||||||||
|
|
|
| ||||||||||
|
|
| |||||||||||
|
| ||||||||||||
|
|
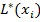
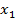
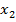
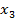
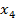
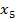
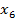
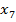
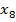
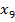
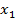
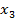
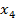
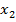
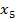
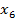
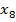
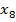
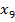
Шаг 1. Начальная вершина 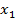имеет постоянную метку 
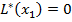, остальные вершины имеют временную метку .
|
|
|
Шаг 2. Определяем множество последователей вершины .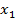
.
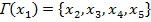Пересчитываем их временные метки по основной формуле:
;
;
.
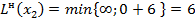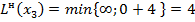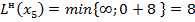Берем вершину 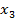с минимальной временной меткой 4, присваиваем этой вершине постоянную метку 
.
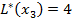Шаг 3. Определяем множество последователей вершины .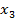
.
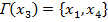Пересчитываем их временные метки по основной формуле:
.
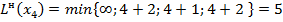Берем вершину 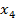с минимальной временной меткой 5, присваиваем этой вершине постоянную метку 
.
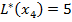Шаг 4. Определяем множество последователей вершины .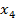
.
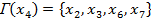Пересчитываем их временные метки по основной формуле:
;
;
.
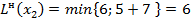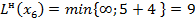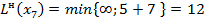Берем вершину 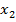с минимальной временной меткой 6, присваиваем этой вершине постоянную метку 
.
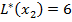Шаг 5. Определяем множество последователей вершины .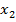
.
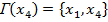Вершины 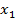и 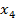уже имеют постоянные метки, поэтому определяем вершину с минимальной временной меткой. Это вершина 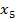. Присваиваем этой вершине постоянную метку 
.
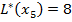Шаг 6. Определяем множество последователей вершины .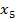
.
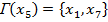Пересчитываем их временные метки по основной формуле:
.
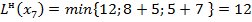Берем вершину 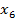с минимальной временной меткой 9, присваиваем этой вершине постоянную метку 
.
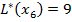Шаг 7. Определяем множество последователей вершины .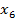
.
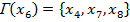Пересчитываем их временные метки по основной формуле:
;
.
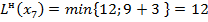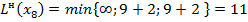Берем вершину 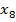с минимальной временной меткой 11, присваиваем этой вершине постоянную метку 
.
|
|
|
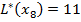Шаг 8. Определяем множество последователей вершины .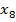
.
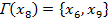Пересчитываем их временные метки по основной формуле:
.
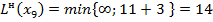Берем вершину 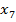с минимальной временной меткой 12, присваиваем этой вершине постоянную метку 
.
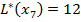Шаг 9. Определяем множество последователей вершины .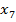
.
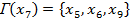Пересчитываем их временные метки по основной формуле:
.
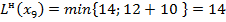Берем вершину 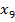с минимальной временной меткой 14, присваиваем этой вершине постоянную метку 
.
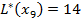Расчеты окончены. Кратчайшие пути найдены, их длина приведена в последних двух столбцах расчетной таблицы.
