Пример IY

Коммерческие банки 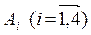на различный срок выделяют кредиты предприятиям 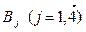под процент 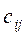с целью получения для себя максимальной прибыли от процентов. Выделяемая сумма кредита банками 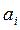, потребность предприятий в кредите 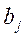(млн ден.ед.) и процентные ставки 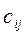из расчета 100 ден. ед. в зависимости от сроков возмещения приведены в матрице:

= .

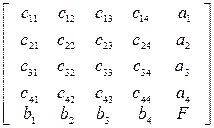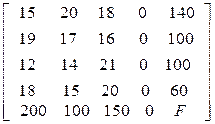Требуется:

1) построить экономико-математическую модель задачи по распределению кредита банками предприятиям с целью получения максимальной прибыли по процентам;

2) методом потенциалов найти оптимальное распределение кредитов, максимизирующее общую прибыль, полученную банками от предприятий;

3) указать предприятия, которые недополучат кредит, а также его сумму.

РЕШЕНИЕ

1) Проверим условие закрытости модели: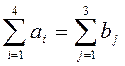

, .

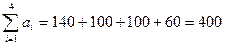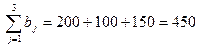Т.о. условие закрытости модели не выполняется, поэтому надо вводить фиктивный банк A₅ с выделяемой суммой кредита а₅ = 50 млн ден. ед. и с процентными ставками С_5j = 0 (j = l,3). После введения фиктивного банка открытая модель задачи преобразовалась в закрытую. Составим распределительную таблицу 10.

Таблица 10

	Предприятия
Банки	В1	В2	В3	Выделенный кредит
A1
А2
А3
А4	I8
А5
Потребность в кредите

Пусть Х_ij - кредиты, выделяемые банком A_i предприятию B_j (i= 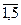; j = ).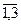

Тогда суммарная прибыль, получаемая банками от предприятий, представлена целевой функцией:

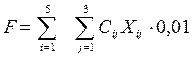. (l)

Система ограничений примет вид:

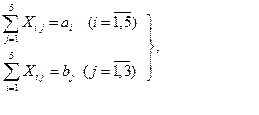(2)

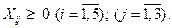(3)

2) Решим поставленную задачу методом потенциалов. Начальный опорный план определим по правилу «максимального» элемента.

Таблица 11

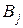
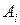
	B1	B2	B3	аi	Ui
А1	_				+	*
A2						16
A3
A4	+					_ 20
A5
bj
Vj

Получен невырожденный опорный план, которому соответствует значение целевой функции:

F₁ =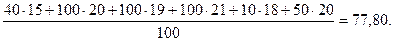

Найдем потенциалы банков и предприятий (из условия, что для каждой загруженной клетки U_i +V_j = с_ij)

U1+ V1 = 15,	U4 + V1 = 18,
U1 + V2 = 20,	U4 + V3 = 20,
U2 +V1 = 19,	U5 + V1 = 0.
U3 + V3 = 21,

Поскольку число уравнений на единицу меньше числа потенциалов, то одному из них придадим произвольное значение. Положим, например, V₁=0. Все остальные потенциалы определяются однозначно:

U₁= 15; U₂ =19; U₃ += 19; U₄ =18; U₅ = 0; V₁= 0; V₂ = 5; V₃ = 2.

Определяем оценки свободных клеток: S_ij = С_ij –(U_i +V_j):

S53 = 0 - (0 + 2) = -2,	S23 = 16 - (19 + 2) = - 5,
S22 = 17 - (19 + 5) = -7,	S13 = 18 - (15 + 2) = 1,
S31 = 12 - (19 + 0) = -7,	S32 = 14 - (19 + 5) = - l 0,
S42 = 15 - (18 + 5) = -8,	S52 = 0 - (0 + 5) = - 5.

Полученный план не оптимален, так как среди оценок свободных клеток имеется положительная S₁₃ =1. Необходимо загрузить клетку (1,3). Построим замкнутый цикл для клетки (1,3).

В отрицательных вершинах цикла наименьшее количество кредита равно

min (40,50) = 40. Получаем новый план распределения кредитов.

Таблица 12

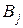
	B1	B2	B3	аi	Ui
A1
A2					16
A3
A4
A5
bj
Vj

Получен опорный план, которому соответствует значение целевой функции:

F₂ =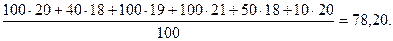

Найдем потенциалы банков и предприятий.

U1+ V2 = 20,	U4 + V1 = 18,
U1 + V3 = 18,	U4 + V3 = 20,
U2 + V1 = 19,	U5 + V1 = 0.
U3 + V3 = 21,

U₁= 16; U₂ =19; U₃ = 19; U₄ =18; U₅ = 0; V₁= 0; V₂ = 4; V₃ = 2.

Определяем оценки свободных клеток.

S11 = 15 - (16 + 0) = -1,	S31 = 12 - (19 + 0) = - 7,
S22 = 17 - (19 + 4) = -5,	S42 = 15 - (18 + 4) = - 7,
S23 = 16 - (19 + 2) = -5,	S52 = 0 - (0 + 4) = - 4,
S53 = 0 - (0 + 2) = -2,	S32 = 14 - (19 + 4) = - 9.

Так как все оценки клеток отрицательные, то полученный план размещения кредитов оптимален, а так как среди оценок нет нулевых, то оптимальный план и единственный.

3) Недополучит кредит предприятие В₁ в объеме 50 млн ден.ед.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Кузнецов, А. В. Высшая математика. Математическое программирование: учебник. / А. В. Кузнецов, В. А Сакович, Н. И. Холод; под общ. ред. А. В. Кузнецова. – 2-е изд., перераб. и доп. – Минск: Выш. шк., 2001. – 351 с.

2. Сборник задач и упражнений по высшей математике. Математическое программирование: учеб. пособие / А.В. Кузнецов, В. А. Сакович, Н. И. Холод и др.; под общ. ред. А. А. Кузнецова, Р. А. Рутковкого. – 2–е изд., перераб. и доп. – Минск: Выш. шк., 2002. – 447 с.

3. Кузнецов, А. В. Руководство к решению задач по математическому программированию: учеб. пособие / А. В. Кузнецов, Н. И. Холод, Л. С. Костевич; под общ. ред. А. В. Кузнецова. – 2–е изд., перераб. и доп. – Минск: Выш. шк., 2001. – 448 с.

4. Костевич, Л. С. Математическое программирование. Информ. технологии оптимальных решений: учебн. пособие / Л. С. Костевич. – Минск: Новое знание, 2003. – 424 с.

5. Курицкий, Б. Я. Поиск оптимальных решений средствами Excel 7.0. / Б. Я. Курицкий. – Санкт–Петербург, 1997. – 384 с.

Учебное издание