Точка 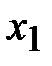 является золотым сечением отрезка
является золотым сечением отрезка 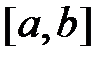 , если отношение длины
, если отношение длины 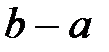 всего отрезка к длине
всего отрезка к длине 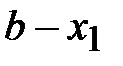 большей части равно отношению большей части к длине меньшей части
большей части равно отношению большей части к длине меньшей части 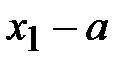 , т. е.
, т. е. 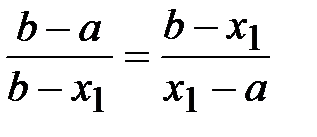 . Аналогично, точка
. Аналогично, точка 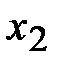 , симметричная точке
, симметричная точке 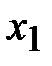 относительно середины отрезка, является вторым золотым сечением этого отрезка.
относительно середины отрезка, является вторым золотым сечением этого отрезка.
Так как точки 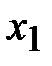 и
и 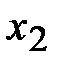 симметричны относительно середины отрезка
симметричны относительно середины отрезка 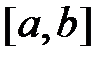 , то можно записать
, то можно записать
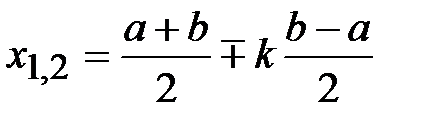 , (8.1)
, (8.1)
где 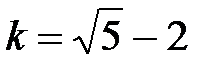 . Свойство золотого сечения: точка
. Свойство золотого сечения: точка 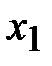 одновременно является золотым сечением отрезка
одновременно является золотым сечением отрезка 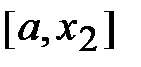 , а другая точка
, а другая точка 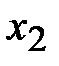 - золотым сечением отрезка
- золотым сечением отрезка 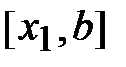 .
.
При поиске минимума функции используется следующий алгоритм:
1. На исходном отрезке 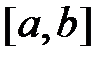 по формуле (8.1) при
по формуле (8.1) при 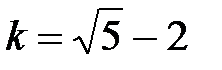 найдем точки
найдем точки 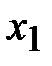 и
и 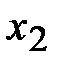 , а затем разность
, а затем разность 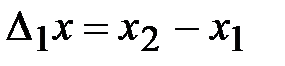 .
.
2. Вычисляются значения функции 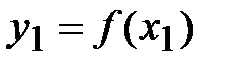 и
и 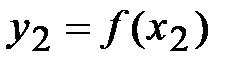 , и по схеме сужения промежутка унимодальности образуется суженный отрезок
, и по схеме сужения промежутка унимодальности образуется суженный отрезок 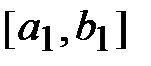 .
.
3. На полученном отрезке 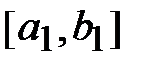 находятся два сечения
находятся два сечения 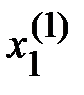 и
и 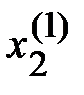 . При этом возможны три случая:
. При этом возможны три случая:
1) 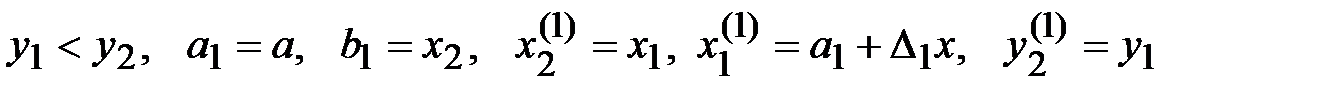 .
.
2) 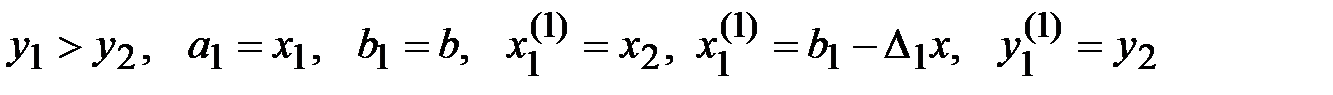 .
.
3) 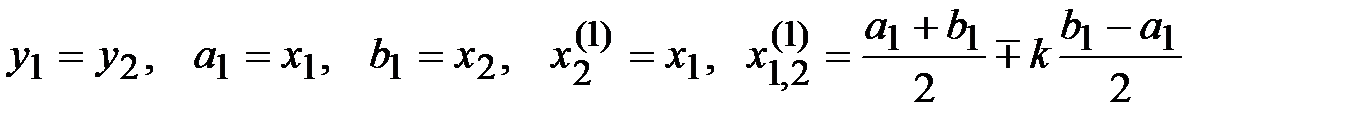 .
.
4. По приведенной схеме находятся отрезки 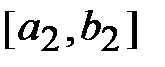 ,
, 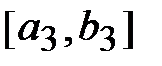 и т. д., с учетом того, что в случаях 1) и 2) значение
и т. д., с учетом того, что в случаях 1) и 2) значение 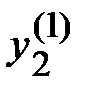 или
или 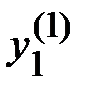 целевой функции уже получено на предыдущем шаге
целевой функции уже получено на предыдущем шаге 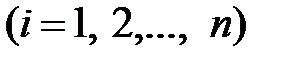 .
.
5. Точность приближенного равенства 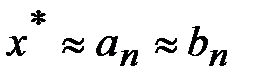 на
на 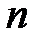 -м шаге вычислений можно оценить неравенством
-м шаге вычислений можно оценить неравенством 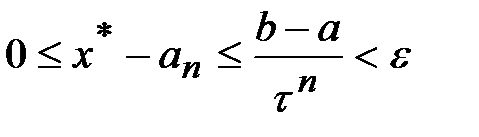 ,
,
где 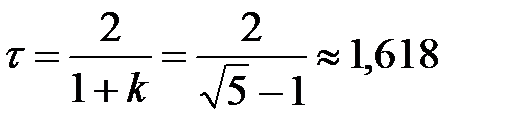 .
.
 2015-04-20
2015-04-20 414
414








