Метод сканирования

Пусть функция 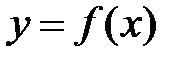является унимодальной на некотором промежутке. Предположим, что произвольная точка 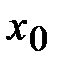этого промежутка является исходной для поиска точки локального минимума и число 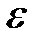- заданная точность нахождения 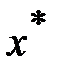. Обозначим через 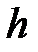произвольное приращение аргумента 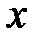и, сделав один шаг от точки 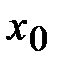, получим новое значение аргумента .

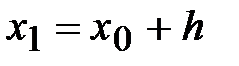Сравним возможные значения функци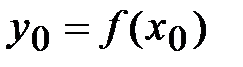и и 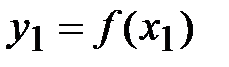. Возможны три варианта продолжения приближения к точке минимума.

1. 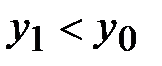- произошло уменьшение значения функции. В качестве нового стартового значения принимается 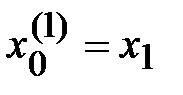. Вычисления по этой схеме продолжаются до тех пор, пока не произойдет увеличение значения функции, т. е. 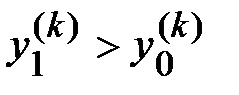, и если при этом 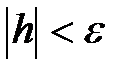, то принимаем 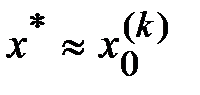с погрешностью 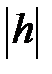. В противном случае полагаем, что точка 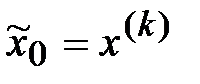является исходной для продолжения вычислений по следующей схеме 2.

2. 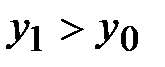- значение функции возросло. В этом случае полагаем, что начальной точкой вычислений является точка 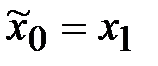, а меньшим шагом для продолжения вычислений – величина 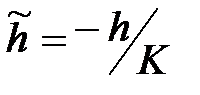, где 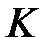- некоторое целое число, 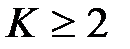. Далее производим вычисления по схеме 1 или 2 до достижения требуемой точности.

3. 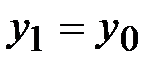(маловероятно). Принимается либо 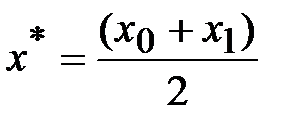при достижении требуемой точности 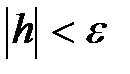, либо следовать схеме 2.

Поиск минимума функции одной переменной данным методом представляет собой колебательный процесс около точки локального минимума функции с непрерывно уменьшающейся амплитудой.

Для определения точки локального минимума метод сканирования применим без предварительного нахождения промежутков унимодальности функции. С помощью метода сканирования можно найти различные точки локального минимума, если целевая функция 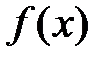имеет не один минимум.