2015-04-20
442
Пусть требуется решить задачу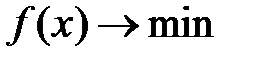 
, 
.
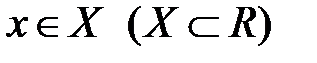Применение численных методов для отыскания точек локального минимума функции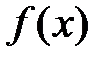 
предполагает:
1) определение промежутков унимодальности функции, то есть нахождение отрезков, которым принадлежит одна точка локального минимума;
2) вычисление значения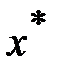 
, принадлежащего выбранному промежутку, с заданной точностью.
При вычислении точки минимума точность достигается последовательным уменьшением отрезка, содержащего точку 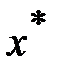, до размеров, не превышающих заданную точность 
(
).
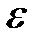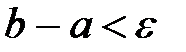Пусть функция 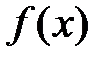унимодальна на отрезке 
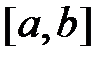. Выбираются две произвольные точки, принадлежащие отрезку 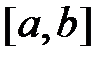, такие, что 
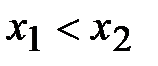. В каждом из следующих трех случаев можно указать отрезок меньших размеров 
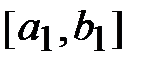, содержащий точку 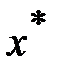и принадлежащий первоначальному отрезку.
1. Если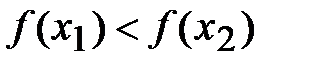 
, то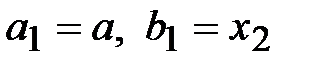 
.
2. Если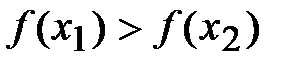 
, то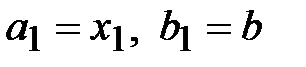 
.
3. Если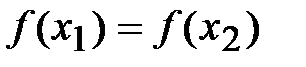 
, то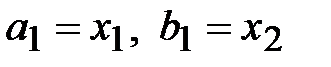 
.
Методы вычисления значения точки минимума функции одной переменной отличаются алгоритмами выбора точек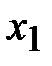 
и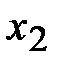 
для локализации точки 
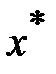с заданной точностью.
