2015-04-30
644
1.5.1 Запишем для цепи, изображенной на рис. 1.7, б, функцию передачи:
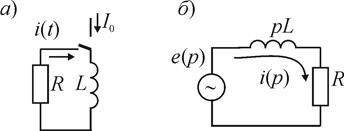
Рис. 1.7
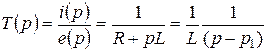, где p 1 = 
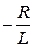(1.12)
Рассмотрим, как протекают свободные колебания в схеме, изображенной на рис. 1.7, а. В индуктивности схемы рис. 1.7, а, когда индуктивность была подключена к источнику тока I 0, запаслась энергия:
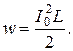
После коммутации ключа к резистору R эта энергия должна в нем рассеяться.
Для отыскания закона изменения тока в контуре запишем в соответствии со вторым законом Кирхгофа:
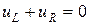(1.13)
; 
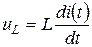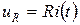(1.14)
Подставив (1.14) в (1.13) получим:
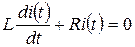(1.15)
Это линейное однородное уравнение первого порядка, решение которого сводится к подбору такой функции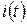 
, производная которой отличалось бы от самой функции лишь постоянным множителем. Таким свойством обладает показательная функция:
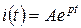
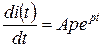(1.16)
Подставив (1.16) в (1.15) получим:
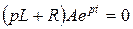(1.17)
Уравнение (1.17) имеет два решения:
1. А = 0 Оно описывает состояние покоя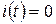 
.
2. 
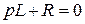, которое имеет решение 
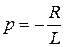(1.18)
Интересно отметить совпадение значений полюса функции передачи схемы рис. 1.7, б (1.12) и решения дифференциального уравнения (1.18).
Приравняв значение тока в момент времени равный нулю к I 0 найдем значение постоянной А = I 0. Тогда частное решение дифференциального уравнения запишем в виде:
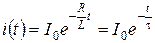, (1.19)
где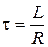 
— называется постоянной времени.
Графически решение (1.19) представлено на рис. 1.8.
Совпадение соотношений (1.12) и (1.18) имеет ясный физический смысл: свободные колебания в линейных L, C, R цепях могут только уменьшаться (затухать) во времени.
Для функций входных, выходных сопротивлений и проводимостей родственные ограничения называются условиями физической реализуемости (УФР):
Вещественные части нулей и полюсов этих функций могут располагаться только в левой части р – плоскости (рис. 1.6). То же самое можно сказать о полюсах передаточных функций.
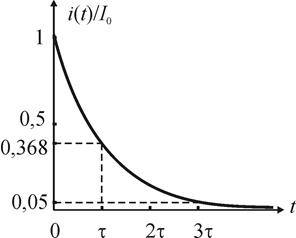
Рис. 1.8
