Последовательный контур и реактансное преобразование частоты

2.1.1 Амплитудно-частотная характеристика (АЧХ) тока в последовательном контуре

Запишем соотношение для тока в последовательном контуре (рис. 2.1):

, (2.1)

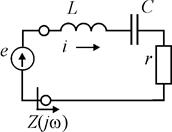
Рис. 2.1

Сопротивление последовательного контура Z (j w):

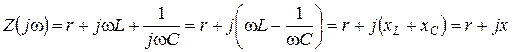, (2.2)

где 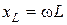— реактивное сопротивление индуктивности,

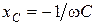— реактивное сопротивление емкости,

x — реактивное сопротивление контура.

Графики составляющих сопротивления последовательного контура показаны на рис. 2.2.

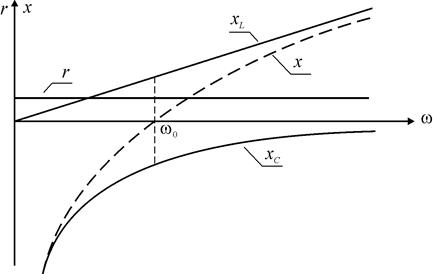
Рис. 2.2

На резонансной частоте w₀ реактивное сопротивление контура x равно нулю:

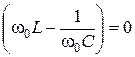, откуда 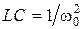, (2.3)

сопротивление контура становится чисто активным и равным r, а ток в контуре равным: 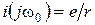(2.4)

Поделим соотношение (2.1) на (2.4) и запишем нормированную функцию:

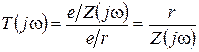. (2.5)

Преобразуем соотношение (2.2) с учетом (2.3):

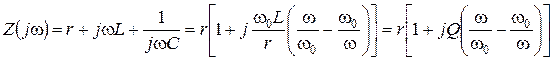,(2.6)

где 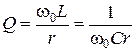— добротность контура.

Поделив на r получим соотношение для нормированного сопротивления контура:

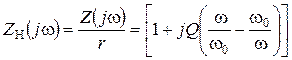(2.7)

Подставим (2.6) в (2.5) и (для того чтобы не затруднять преобразования выражениями в радикалах) запишем квадрат модуля полученного соотношения:

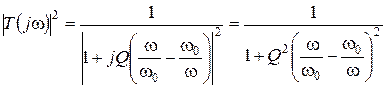(2.8)

График полученной зависимости показан на рис. 2.3.

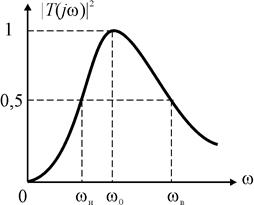
Рис. 2.3

Отсчитывая верхнюю и нижнюю 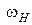граничные частоты и полосу пропускания контура 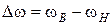по уровню, когда мощность в сопротивлении 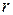уменьшится в два раза, найдем эти величины:

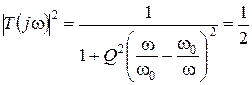(2.9)

Откуда 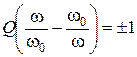или

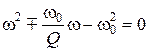(2.10)

Решение уравнения (2.10):

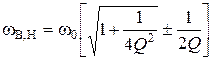(2.11)

Откуда: 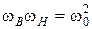, (2.12)

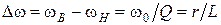и 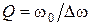(2.13)

Можно показать, что произведение частот, отсчитанных на любой высоте от 0 до 1 от оси частот, всегда будет удовлетворять соотношению (2.12). Такой вид симметрии характеристик называют геометрической симметрией [15].

В дальнейшем, используем для обозначения текущей частоты этого простейшего ППФ индекс «пф» 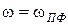, и преобразуем соотношения (2.7) и (2.8), подставив в них значение Q из (2.13):

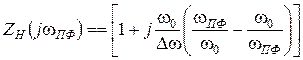(2.14)

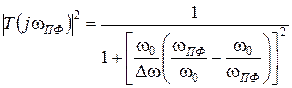(2.15)

Если ввести нормированную переменную 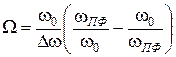, (2.16)

Атабеков [2] называет ее 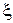— обобщенной расстройкой контура, (разрядка Атабекова; см. изд. 1969г.) соотношения (2.14) и (2.15) можно переписать:

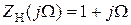(2.17)

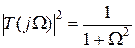(2.18)

Соотношения (2.17) и (2.18) описывают простейший фильтр нижних частот (ФНЧ) с нормированными значениями индуктивности 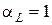и активного сопротивления r_Н = 1, изображенный на рис. 2.4 а. Составляющие его входного сопротивления (2.17) показаны на рис. 2.4, б, а квадрат модуля функции передачи — на рис. 2.4, в.

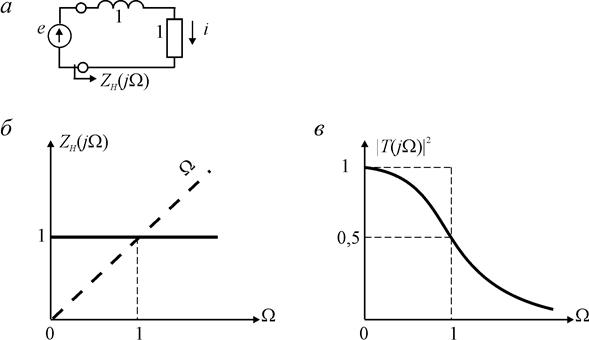
Рис. 2.4

Нормированную переменную ФНЧ 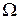можно представить также как отношение текущей частоты ФНЧ 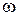к частоте среза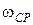

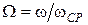(2.19)

2.1.2 Если приравнять частоту среза ФНЧ 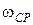к полосе пропускания ППФ 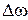, из соотношений (2.16), (2.19) можно найти связь частотных переменных ФНЧ 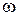и ППФ

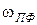
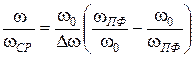Þ 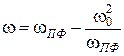(2.20)

Используя замены переменных 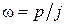и 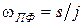установим связь между комплексными частотами ФНЧ и ППФ

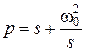(2.21)

Соотношение (2.21) позволяет найти структуру и величины элементов ППФ, если известна структура и величины элементов ФНЧ, например:

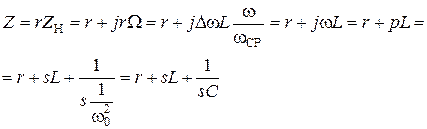(2.22)

здесь также как в (2.3) 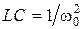. Преобразования иллюстрирующие соотношение (2.22) показаны на рис. 2.5.

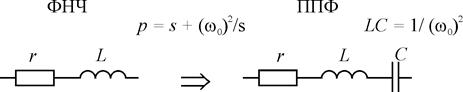
Рис. 2.5

В общем случае каждая индуктивность ФНЧ превращается в последовательный контур ППФ настроенный на частоту 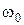, а каждая емкость ФНЧ — в параллельный контур, настроенный на частоту 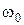.(рис. 2.6).

Рис. 2.6

При этом полоса пропускания ППФ равна частоте среза ФНЧ, а вид и характерные точки АЧХ ППФ соответствуют (легко вычисляются по соотношению (2.20)) АЧХ ФНЧ.

Связь частотных характеристик ФНЧ и ППФ иллюстрируют графики на рис. 2.7, построенные с помощью соотношения (2.16).

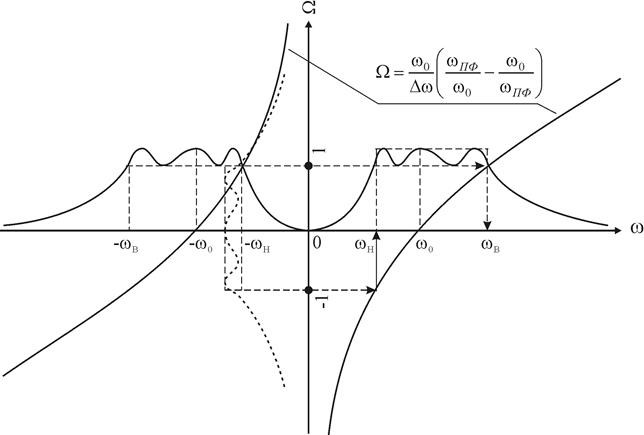
Рис. 2.7 Связь частотных характеристик ФНЧ (пунктирная кривая) и ППФ

2.1.3 Рассмотрим пример расчета полосового трехконтурного фильтра
(n = 3) с максимально-гладкой АЧХ и следующими характеристиками:

- полоса пропускания 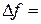6 МГц;

- средне-геометрическая частота полосы пропускания f ₀ = 60 МГц;

- сопротивление нагрузки (и сопротивление генератора) R = 75 Ом.

Для расчета используем фильтр-прототип нижних частот, показанный на рис. 1.13 а. Приравняем в соответствии с соотношением (2.20) частоты среза ФНЧ и ППФ 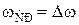и рассчитаем сначала фильтр нижних частот, используя соотношения (1.23):

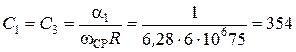пФ,

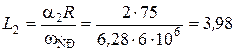мкг.

Схемы фильтра-прототипа с нормированными элементами и ФНЧ, а также их частотные характеристики приведены на рисунках 2.8 а —2.8 г.

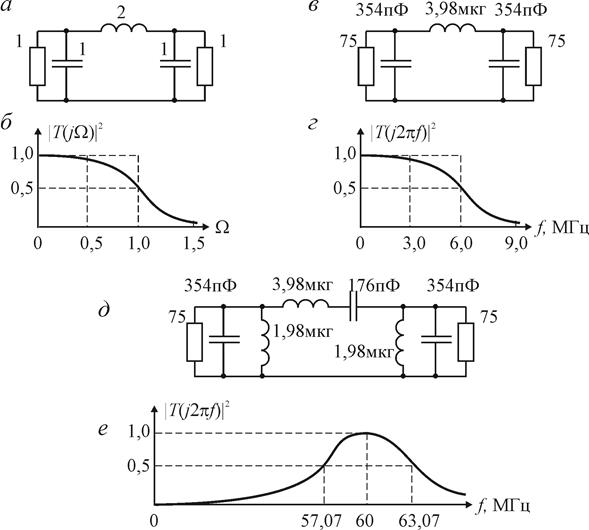
Рис. 2.8

Для того чтобы ФНЧ превратить в ППФ достаточно подключить параллельно к каждому конденсатору ФНЧ катушку индуктивности, а последовательно с каждой катушкой индуктивности ФНЧ — конденсатор. Все контура и параллельные и последовательные должны быть настроены на частоту 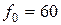МГц. Схема рассчитанного ППФ и его частотная характеристика приведены
на рис. 2.8 д и рис.2.8 е.